Phương pháp giải:

Tính tỉ lệ thể tích khối tứ diện \(SGCD\) và khối chóp \(S.ABCD\).

Lời giải chi tiết:

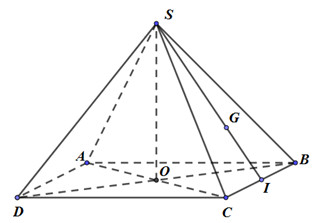
Gọi I là trung điểm của BC, do \(G\) là trọng tâm tam giác \(SBC \Rightarrow \dfrac{{SG}}{{SI}} = \dfrac{2}{3}\).

Ta có: \(\dfrac{{{V_{SGCD}}}}{{{V_{SICD}}}} = \dfrac{{SG}}{{SI}} = \dfrac{2}{3}\).

\({S_{\Delta DIC}} = \dfrac{1}{4}{S_{ABCD}} \Rightarrow {V_{S.CDI}} = \dfrac{1}{4}{V_{S.ABCD}} \Rightarrow {V_{SGCD}} = \dfrac{2}{3}.\dfrac{1}{4}{V_{S.ABCD}} = \dfrac{1}{6}{V_{S.ABCD}}\)

Ta có:

\(\begin{array}{l}OC = \dfrac{1}{2}AC = \dfrac{{\sqrt 2 }}{2},\,\,SO = \sqrt {S{C^2} - O{C^2}}  = \sqrt {1 - \dfrac{1}{2}}  = \dfrac{{\sqrt 2 }}{2}\\ \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{\sqrt 2 }}{2}{.1^2} = \dfrac{{\sqrt 2 }}{6} \Rightarrow {V_{SGCD}} = \dfrac{1}{6}.\dfrac{{\sqrt 2 }}{6} = \dfrac{{\sqrt 2 }}{{36}}\end{array}\)

Chọn: A