Phương pháp giải:

+) Xác định vị trí của điểm H.

+) Dựa vào phương pháp xác định góc giữa hai mặt phẳng để xác định góc giữa hai mặt phẳng (SBC) và (ABC).

+) Sử dụng hàm tan tính tan của góc vừa xác định được.

Lời giải chi tiết:

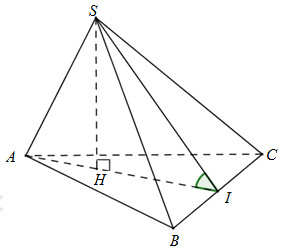
Ta có: \(\overrightarrow {IH}  + 2\overrightarrow {AH}  = \overrightarrow 0 \) nên H nằm giữa A; I và \(HI = 2AH.\)

Vì tam giác ABC đều nên \(AI \bot BC\).

Mà \(SH \bot BC \Rightarrow BC \bot \left( {SHI} \right) \Rightarrow BC \bot SI\)

\(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SI \bot BC\\AI \bot BC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SI;AI} \right)} = \widehat {SIA}\)  (\(\widehat {SIA} < {90^0}\))

Ta có: \(AI = a\sqrt 2 .\frac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{2};HI = \dfrac{2}{3}AI = \dfrac{{a\sqrt 6 }}{3}\)

Xét tam giác vuông SHI có: \(\tan \widehat {SIH} = \dfrac{{SH}}{{IH}} = 2a\dfrac{3}{{a\sqrt 6 }} = \sqrt 6 \)

Chọn A.