Câu hỏi:
Cho chóp S.ABC có đáy là tam giác vuông cân tại A có cạnh góc vuông là \(a\sqrt 2 \), SA vuông góc với đáy và \(SA = a\). Tính góc giữa hai mặt phẳng \(\left( {SBC} \right)\)và \(\left( {ABC} \right)\)?
- A \({30^0}\)
- B \({45^0}\)
- C \({60^0}\)
- D \({90^0}\)
Phương pháp giải:
Gọi I là trung điểm của BC. Chứng minh AI và SI cùng vuông góc với giao tuyến BC.
Lời giải chi tiết:
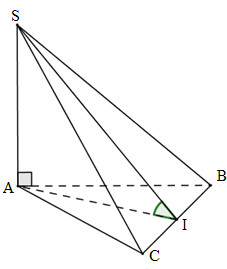
Gọi I là trung điểm của BC
Vì tam giác ABC vuông cân tại A nên \(AI \bot BC\) và \(AI = \frac{{BC}}{2} = \frac{{a\sqrt 2 .\sqrt 2 }}{2} = a\)
\(\Delta SAC = \Delta SAB\left( {c.g.c} \right) \Rightarrow SB = SC \Rightarrow \Delta SBC\)cân tại S\( \Rightarrow SI \bot BC\)
\(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SI \bot BC\\AI \bot BC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SI;AI} \right)} = \widehat {SIA}\)
Xét tam giác vuông SAI có: \(\tan \widehat {SIA} = \frac{{SA}}{{AI}} = \frac{a}{a} = 1 \Rightarrow \widehat {SIA} = {45^0}\)
Chọn B.


















