Câu hỏi:
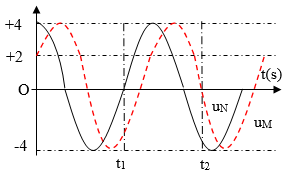
Sóng ngang có tần số f truyền trên một sợi dây đàn hồi rất dài, với tốc độ 4,5m/s. Xét hai điểm M và N trên cùng một phương truyền sóng, cách nhau một khoảng x nhỏ hơn một bước sóng, sóng truyền từ N đến M. Đồ thị biểu diễn li độ sóng của M và N cùng theo thời gian như hình vẽ. Biết t1=0,05s. Tại t2, khoảng cách giữa phần tử chất lỏng tại M và N có giá trị gần giá trị nào nhất sau đây?
- A 4,8cm
- B 6,2cm
- C 5,7cm
- D 3,5cm
Phương pháp giải:
Lời giải chi tiết:
Từ đồ thị ta thấy N sớm pha hơn M một góc \(\frac{\pi }{3}\); \(\frac{{2\pi MN}}{\lambda } = \frac{\pi }{3} \to MN = \frac{\lambda }{6}\);
xác định được \(\frac{T}{4} + \frac{T}{2} = 0,05s \to T = \frac{1}{{15}}s \to \lambda = v.T = 30cm \to MN = 5cm\);
\({u_M} = 4\cos \left( {\omega t - \frac{\pi }{3}} \right)cm\); \({u_N} = 4\cos \omega tcm\);
với \({t_2} = {t_1} + \frac{T}{2} + \frac{T}{6}\)ta xác định được \({\left| {{u_M} - {u_N}} \right|_{t = {t_2}}} = 2\sqrt 3 cm \to M{N_{t = {t_2}}} = \sqrt {{5^2} + {2^2}.3} = \sqrt {37} = 6,082\)cm
Chọn B