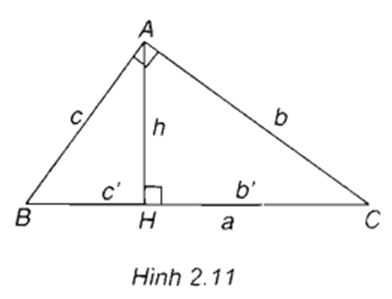
Câu hỏi 1 trang 46 SGK Hình học 10

Đề bài

Tam giác \(ABC\) vuông tại \(A \) có đường cao \(AH = h\) và có  \(BC = a, CA = b, AB = c\). Gọi \(BH = c’\) và \(CH = b’\) (h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:

\(a^2 = b^2+ (...)\)

 \(b^2=a.(...)\)

\(c^2=a.(...)\)

 \(h^2=b'.(...)\)

\(a.h = b . (...)\)

\(\eqalign{
& {1 \over {...}} = {1 \over {{b^2}}} + {1 \over {{c^2}}} \cr
& \sin B = \cos C = { ...\over a} \cr
& \sin C = \cos B = { ...\over a} \cr
& \tan B = \cot C = {... \over c} \cr
& \cot B = \tan C = {... \over b} \cr} \)

Lời giải chi tiết

\(a^2 = b^2+ c^2\)

 \(b^2=a.b'\)

\(c^2=a.c'\)

 \(h^2=b'.c'\)

\(a.h = b . c\)

\(\eqalign{
& {1 \over {{h^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}} \cr
& \sin B = \cos C = {b \over a} \cr
& \sin C = \cos B = {c \over a} \cr
& \tan B = \cot C = {b \over c} \cr
& \cot B = \tan C = {c \over b} \cr} \)

Loigiaihay.com