Cho ngũ giác đều \(ABCDE\). Gọi \(K\) là giao điểm của \(AC\) và \(BE\) . Khi đó hệ thức nào dưới đây là đúng?
-
A.
\(C{B^2} = AK.AC\)
-
B.
\(O{B^2} = AK.AC\)
-
C.
\(AB + BC = AC\)
-
D.
Cả A, B, C đều sai.
Sử dụng tam giác đồng dạng
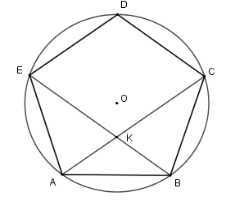
Vì \(AB = AE\) (do \(ABCDE\) là ngũ giác đều ) nên cung \(AB = \) cung \(AE\)
Xét tam giác \(AKB\) và tam giác \(ABC\) có
\(\widehat A\) chung và \(\widehat {KBA} = \widehat {KCB}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB,AE\) )
Suy ra \(\Delta AKB\backsim\Delta ABC\left( {g - g} \right)\)
\(\Rightarrow \dfrac{{AK}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow A{B^2} = AK.AC\) .
Mà $AB = BC$ nên \(B{C^2} = AK.AC\) .
Theo bất đẳng thức tam giác thì \(AB + BC > AC\) nên C sai
Vì \(ABCDE\) là ngũ giác đều nên \(BC \ne OB\) nên B sai.
Đáp án : A
Các bài tập cùng chuyên đề
Đường tròn ngoại tiếp đa giác là đường tròn
Số đường tròn nội tiếp của một đa giác đều là
Đường tròn nội tiếp hình vuông cạnh \(a\) có bán kính là
Cho lục giác đều \(ABCDEF\) nội tiếp đường tròn tâm \(O\) . Tính số đo góc \(AOB\) .
Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính \(4\,cm\) (làm tròn đến chữ số thập phân thứ nhất)
Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính \(4\,cm\) (làm tròn đến chữ số thập phân thứ nhất).
Tính cạnh của hình vuông nội tiếp \(\left( {O;R} \right)\)
Tính độ dài cạnh của tam giác đều nội tiếp \(\left( {O;R} \right)\) theo \(R.\)
Cho \(\left( {O;4} \right)\) có dây \(AC\) bằng cạnh hình vuông nội tiếp và dây \(BC\) bằng cạnh tam giác đều nội tiếp đường tròn đó ( điểm \(C\) và \(A\) nằm cùng phía với \(BO\) ). Tính số đo góc \(ACB\)
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số $\dfrac{R}{r}$ là:
Bát giác đều ABCDEFGH nội tiếp đường tròn bán kính bằng 1. Tính độ dài cạnh AB của bát giác.
