Đề bài

Cho \(\left( {O;4} \right)\)  có dây \(AC\) bằng cạnh hình vuông nội tiếp và dây \(BC\) bằng cạnh tam giác đều nội tiếp đường tròn đó ( điểm \(C\) và \(A\) nằm cùng phía với \(BO\) ). Tính số đo góc \(ACB\) 

• A.  \(30^\circ \) 
• B. \(45^\circ \)  
• C. \(60^\circ \) 
• D. \(15^\circ \) 

Phương pháp giải

+ Tìm số đo các cung \(BC\) và \(AB\) để tìm số đo cung \(AC\)

+ Sử dụng: số đo góc nội tiếp bằng nửa số đo cung bị chắn

Lời giải của GV Loigiaihay.com

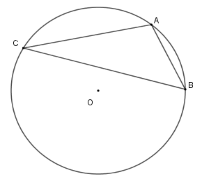
+ Vì \(AC\) bằng cạnh của hình vuông nội tiếp \(\left( O \right)\) nên số đo cung \(AC = 90^\circ \)

Vì \(BC\) bằng cạnh của tam giác đều nội tiếp \(\left( O \right)\) nên số đo cung \(BC = 120^\circ \)

Từ đó suy ra số đo cung \(AB = 120^\circ  - 90^\circ  = 30^\circ \)

+ Vì \(\widehat {ACB}\) là góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \dfrac{{30^\circ }}{2} = 15^\circ \) 

Đáp án : D

Chú ý

Một số em nhớ nhầm lý thuyết (số đo góc nội tiếp bằng số đo cung bị chắn) dẫn đến ra phương án A sai.