Giải phương trình \(5{{x}^{4}}+2{{x}^{2}}-16=10-{{x}^{2}}\)
-
A.
\(x=\sqrt{2}\)
-
B.
\(x=\pm \sqrt{2}\)
-
C.
\(x=-\sqrt{2}\)
-
D.
\(x=2\)
Thu gọn phương trình ban đầu về phương trình trùng phương. Đặt \({{x}^{2}}=t\,\,(t\ge 0)\) đưa phương trình trùng phương ban đầu về phương trình bậc hai. Giải phương trình bậc hai tìm t, kết hợp với điều kiện, tìm x ban đầu.
\(5{{x}^{4}}+2{{x}^{2}}-16=10-{{x}^{2}} \\ 5{{x}^{4}}+3{{x}^{2}}-26=0\)
Đặt \({{x}^{2}}=t\,\,\,\left( t\ge 0 \right)\)
Phương trình trở thành \(5{{t}^{2}}+3t-26=0\,\,\left( * \right)\)
Biệt thức \(\Delta ={{3}^{2}} - 4.5.(-26) = 529 > 0\).
PT (*) có 2 nghiệm phân biệt:
\({{t}_{1}}=\frac{-3+\sqrt{529}}{2.5}=2\ \ \left( tm \right) \); \({{t}_{2}}=\frac{-3-\sqrt{529}}{2.5}=\frac{-13}{5}\ \ \left( ktm \right) \)
Với \(t=2\) thì \({{x}^{2}}=2\). Khi đó \(x=\pm \sqrt{2}.\)
Phương trình có 2 nghiệm phân biệt: \(x=\pm \sqrt{2}\)
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Tìm điều kiện của tham số $m$ để phương trình \(m{x^2} - 2(m - 1)x + m - 3 = 0\) có nghiệm.
-
A.
$m \ge 1$
-
B.
$m > 1$
-
C.
$m \ge - 1$
-
D.
$m \le - 1$
Bài 2 :
Biết rằng phương trình ${x^2} - {\rm{ }}2(3m + 2)x + {\rm{ }}2{m^2} - 3m - 10 = 0$
có một trong các nghiệm bằng $ - 1$. Tìm nghiệm còn lại với $m > 0$
-
A.
$x = 11$
-
B.
$x = - 11$
-
C.
$x = 10$
-
D.
$x = - 10$
Bài 3 :
Cho phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$ có biệt thức $b = 2b';\Delta ' = b{'^2} - ac$. Phương trình đã cho có hai nghiệm phân biệt khi
-
A.
$\Delta ' > 0$
-
B.
$\Delta ' = 0$
-
C.
$\Delta ' \ge 0$
-
D.
$\Delta ' \le 0$
Bài 4 :
Cho phương trình bậc hai một ẩn $a{{x}^{2}}+bx+c=0\left( a\ne 0 \right)$, với $b=2b'$ và biệt thức $\Delta '=b{{'}^{2}}-ac$. Nếu $\Delta ' = 0$ thì
-
A.
Phương trình có hai nghiệm phân biệt
-
B.
Phương trình có nghiệm kép ${x_1} = {x_2} = - \dfrac{b}{a}$
-
C.
Phương trình có nghiệm kép ${x_1} = {x_2} = - \dfrac{{b'}}{a}$
-
D.
Phương trình có nghiệm kép ${x_1} = {x_2} = - \dfrac{{b'}}{{2a}}$
Bài 5 :
Tính $\Delta '$ và tìm số nghiệm của phương trình \(7{x^2} - 12x + 4 = 0\) .
-
A.
$\Delta ' = 6$ và phương trình có hai nghiệm phân biệt
-
B.
$\Delta ' = 8$ và phương trình có hai nghiệm phân biệt
-
C.
$\Delta ' = 8$ và phương trình có nghiệm kép
-
D.
$\Delta ' = 0$ và phương trình có hai nghiệm phân biệt
Bài 6 :
Tính $\Delta '$ và tìm nghiệm của phương trình \(2{x^2} + 2\sqrt {11} x + 3 = 0\) .
-
A.
$\Delta ' = 5$ và phương trình có hai nghiệm ${x_1} = {x_2} = \dfrac{{\sqrt 1 1}}{2}$
-
B.
$\Delta ' = 5$ và phương trình có hai nghiệm ${x_1} = \dfrac{- 2\sqrt {11} + \sqrt 5}{2}$ ;${x_2} = \dfrac{-2 \sqrt {11} - \sqrt 5}{2}$
-
C.
$\Delta ' = \sqrt 5 $ và phương trình có hai nghiệm ${x_1} = \sqrt {11} + \sqrt 5 ;{x_2} = \sqrt {11} - \sqrt 5 $
-
D.
$\Delta ' = 5$ và phương trình có hai nghiệm ${x_1} = \dfrac{- \sqrt {11} + \sqrt 5}{2}$ ;${x_2} = \dfrac{- \sqrt {11} - \sqrt 5}{2}$
Bài 7 :
Cho phương trình \(m{x^2} - 2\left( {m - 1} \right)x + m - 3 = 0\). Với giá trị nào dưới đây của $m$ thì phương trình không có hai nghiệm phân biệt.
-
A.
$m = - \dfrac{5}{4}$
-
B.
$m = \dfrac{1}{4}$
-
C.
$m = \dfrac{5}{4}$
-
D.
$m = - \dfrac{1}{4}$
Bài 8 :
Trong trường hợp phương trình \( - {x^2} + 2mx - {m^2} - m = 0\) có hai nghiệm phân biệt. Hai nghiệm của phương trình là
-
A.
${x_1} = m - \sqrt { - m} ;{x_2} = m + \sqrt { - m} $
-
B.
${x_1} = m - \sqrt m ;{x_2} = m + \sqrt m $
-
C.
${x_1} = m - 2\sqrt { - m} ;{x_2} = m + 2\sqrt { - m} $
-
D.
${x_1} = 2m - \sqrt { - m} ;{x_2} = 2m + \sqrt { - m} $
Bài 9 :
Tìm điều kiện của tham số m để phương trình \(m{x^2} + 2\left( {m + 1} \right)x + 1 = 0\) có nghiệm.
-
A.
\(m \ne 0\)
-
B.
\(m < 0\)
-
C.
\(m > 0\)
-
D.
\(m \in \mathbb{R}\)
Bài 10 :
Biết rằng phương trình \(m{x^2} - 4\left( {m - 1} \right)x + 4m + 8 = 0\) có một trong các nghiệm bằng \(3\). Tìm nghiệm còn lại của phương trình.
-
A.
\(x = - \dfrac{6}{5}\)
-
B.
\(x = - 3\)
-
C.
\(x = \dfrac{5}{6}\)
-
D.
\(x = \dfrac{6}{5}\)
Bài 11 :
Cho phương trình \(a{x^2} + bx + c = 0\,\,(a \ne 0)\) có biệt thức \(b = 2b';\Delta ' = b{'^2} - ac\). Phương trình đã cho vô nghiệm khi
-
A.
\(\Delta ' > 0\)
-
B.
\(\Delta ' = 0\)
-
C.
\(\Delta ' \ge 0\)
-
D.
\(\Delta ' < 0\)
Bài 12 :
Tính \(\Delta '\) và tìm số nghiệm của phương trình \(16{x^2} - 24x + 9 = 0\) .
-
A.
\(\Delta ' = 432\) và phương trình có hai nghiệm phân biệt
-
B.
\(\Delta ' = - 432\) và phương trình vô nghiệm
-
C.
\(\Delta ' = 0\) và phương trình có nghiệm kép
-
D.
\(\Delta ' = 0\) và phương trình có hai nghiệm phân biệt
Bài 13 :
Tính \(\Delta '\) và tìm nghiệm của phương trình \(3{x^2} - 2x = {x^2} + 3\) .
-
A.
\(\Delta ' = 7\) và phương trình có hai nghiệm \({x_1} = {x_2} = \dfrac{{\sqrt 7 }}{2}\)
-
B.
\(\Delta ' = 7\) và phương trình có hai nghiệm \({x_1} = \dfrac{{1 + \sqrt 7 }}{2};{x_2} = \dfrac{{1 - \sqrt 7 }}{2}\)
-
C.
\(\Delta ' = \sqrt 7 \) và phương trình có hai nghiệm \({x_1} = \dfrac{{1 + \sqrt 7 }}{2};{x_2} = \dfrac{{1 - \sqrt 7 }}{2}\)
-
D.
\(\Delta ' = 7\) và phương trình có hai nghiệm \({x_1} = \dfrac{{ - 1 + \sqrt 7 }}{2};{x_2} = \dfrac{{ - 1 - \sqrt 7 }}{2}\)
Bài 14 :
Cho phương trình \((m + 1){x^2} - 2(m + 1)x + 1 = 0\). Tìm các giá trị của \(m\) để phương trình có hai nghiệm phân biệt.
-
A.
\(m > 0\)
-
B.
\(m < - 1\)
-
C.
\( - 1 < m < 0\)
-
D.
Cả A và B đúng
Bài 15 :
Trong trường hợp phương trình \({x^2} - 2\left( {m - 2} \right)x + 2m - 5 = 0\) có hai nghiệm phân biệt. Hai nghiệm của phương trình là
-
A.
\({x_1} = \dfrac{2m-5}{2}\) ; \({x_2} = \dfrac{1}{2}\).
-
B.
\({x_1} = 2m-5 \) ; \({x_2} = 1 \).
-
C.
\({x_1} =2m+5 \) ; \({x_2} = -1\).
-
D.
\({x_1} = - m + 3 \) ; \({x_2} = - 5 \).
Bài 16 :
Cho hai phương trình \({x^2} - 13x + 2m = 0\) (1) và \({x^2} - 4x + m = 0\) (2). Xác định \(m\) để một nghiệm phương trình (1) gấp đôi \(1\) nghiệm phương trình (2).
-
A.
\( - 45\)
-
B.
\( - 5\)
-
C.
\(0\) và \( - 5\)
-
D.
Đáp án khác
Bài 17 :
Với giá trị nào của m thì hệ phương trình sau có nghiệm duy nhất \(\left\{ \begin{array}{l}x + y = 8\\\dfrac{x}{y} + \dfrac{y}{x} = m\end{array} \right.\)
-
A.
\(m = 4\)
-
B.
\(m = - 2\)
-
C.
\(m = 2\)
-
D.
\(m = 1\)
Bài 18 :
Tìm m để phương trình \({x^2} + 3x - m = 0\) có nghiệm
-
A.
\(\displaystyle m \ge - {9 \over 4}\)
-
B.
\(\displaystyle m \le {9 \over 4}\)
-
C.
\(\displaystyle m \le {- 9 \over 4}\)
-
D.
Cả A và B
Bài 19 :
Biệt thức \(\Delta '\) của phương trình \(3{x^2} - 2mx - 1 = 0\) là
-
A.
\({m^2} + 3.\)
-
B.
\(4{m^2} + 12\).
-
C.
\({m^2} - 3.\)
-
D.
\(4{m^2} - 12.\)
Bài 20 :
Giải phương trình \({x^2} + 28x - 128 = 0\)
-
A.
\(S = \left\{ { - 32;\,4} \right\}\)
-
B.
\(S = \left\{ {32;\,4} \right\}\)
-
C.
\(S = \left\{ { - 32;\, - 4} \right\}\)
-
D.
\(S = \left\{ {32;\, - 4} \right\}\)
Bài 21 :
Cho Parabol \((P):y=\dfrac{1}{4}{{x}^{2}}\) và đường thẳng \((d):y=mx-2m+1\). Tìm m để (P) và (d) tiếp xúc nhau.
-
A.
m = – 2
-
B.
m = 2
-
C.
m = – 1
-
D.
m = 1
Bài 22 :
Cho Parabol (P): \(y={{x}^{2}}\) và đường thẳng (d): \(y=2(m+1)x-{{m}^{2}}-9\). Tìm m để (d) tiếp xúc với (P).
-
A.
\(m=-4\)
-
B.
\(m>-4\)
-
C.
\(m<-4\)
-
D.
\(m=4\)
Bài 23 :
Cho parabol \(\left( P \right): y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( { - 2;4} \right)\) và tiếp xúc với đồ thị của hàm số \(y = 2(m - 1)x - (m - 1)\).Toạ độ tiếp điểm là
-
A.
\(\left( {0;0} \right)\)
-
B.
\(\left( {1;1} \right)\)
-
C.
A và B đúng
-
D.
Đáp án khác
Bài 24 :
Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình sau:
a) \(3{x^2} + 8x - 3 = 0\);
b) \({x^2} + 6\sqrt 2 x + 2 = 0\).
Bài 25 :
Giải bài toán trong tình huống mở đầu.
Tình huống mở đầu: Trên một mảnh đất hình chữ nhật có kích thước 28m x 16m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là \(288{m^2}\)?
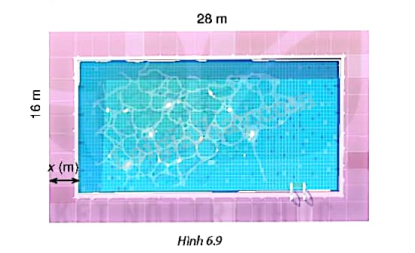
Bài 26 :
Giải bài toán trong tình huống mở đầu.
Tình huống mở đầu: Bác An có 40m hàng rào lưới thép, Bác muốn dùng nó để rào xung quanh một mảnh đất trống (đủ rộng) thành một mảnh vườn hình chữ nhật có diện tích \(96{m^2}\) để trồng rau. Tính chiều dài và chiều rộng của mảnh vườn đó.

Bài 27 :
Giải các phương trình sau:
a) \(5{x^2} - 6\sqrt 5 x + 2 = 0\);
b) \(2{x^2} - 2\sqrt 6 x + 3 = 0\).
Bài 28 :
Nhu cầu của khách hàng đối với một loại áo phông tại một cửa hàng được cho bởi phương trình \(p = 100 - 0,02x\), trong đó p là giá tiền của mỗi chiếc áo (nghìn đồng) và x là số lượng áo phông bán được. Doanh thu R (nghìn đồng) khi bán được x chiếc áo phông là: \(R = xp = x\left( {100 - 0,02x} \right)\). Hỏi cần phải bán được bao nhiêu chiếc áo phông để doanh thu đạt 120 triệu đồng?
Bài 29 :
Dùng công thức nghiệm thu gọn giải các phương trình sau:
a) \(5{x^2} - 12x + 4 = 0\)
b) \(5{x^2} - 2\sqrt 5 x + 1 = 0\)
Bài 30 :
Xét phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) với \(b = 2b'\).
a) Đặt \(\Delta ' = b{'^2} - ac\), chứng tỏ rằng \(\Delta = 4\Delta '.\)
b) Xét tính có nghiệm và nêu công thức nghiệm (nếu có) của phương trình trong các trường hợp: \(\Delta ' > 0;\Delta ' = 0;\Delta ' < 0.\)


















Danh sách bình luận