Cho tam giác $ABC$ có $\widehat B = 60^\circ $, đường trung tuyến $AM$, đường cao $CH$. Vẽ đường tròn ngoại tiếp $BHM$. Kết luận nào đúng khi nói về các cung $HB;MB;MH$ của đường tròn ngoại tiếp tam giác $MHB$ ?
-
A.
Cung $HB$ nhỏ nhất
-
B.
Cung $MB$ lớn nhất
-
C.
Cung $MH$ nhỏ nhất
-
D.
Ba cung bằng nhau
Sử dụng mối liên hệ giữa cung và dây
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
Hai cung bằng nhau căng hai dây bằng nhau và ngược lại
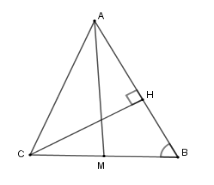
Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng $HB;MB;MH$.
Xét tam giác $BCH$ vuông tại $H$ có $\cos B = \dfrac{{HB}}{{BC}} \Leftrightarrow \dfrac{{HB}}{{BC}} = \cos 60^\circ = \dfrac{1}{2} \Rightarrow HB = \dfrac{{BC}}{2} = BM = CM$
Xét tam giác $HBM$ có $BM = BH$ (cmt) và $\widehat {ABC} = 60^\circ $ nên $\Delta HBM$ là tam giác đều
$ \Rightarrow BM = BH = HM$
Suy ra ba cung $HB;MB;MH$ bằng nhau.
Đáp án : D
Các bài tập cùng chuyên đề
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
Chọn khẳng định đúng.
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
Cho đường tròn $\left( {O;R} \right)$ và hai dây $AB;CD$ sao cho $\widehat {AOB} = 120^\circ ;\widehat {COD} = 60^\circ $. So sánh các dây $CD;AB$.
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 3 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là đúng?
