Đề bài

Cho đường tròn $\left( {O;R} \right)$ và hai dây $AB;CD$ sao cho $\widehat {AOB} = 120^\circ ;\widehat {COD} = 60^\circ $. So sánh các dây $CD;AB$.

• A. $CD = 2AB$
• B. $AB > 2CD$
• C. $CD > AB$
• D. $CD < AB < 2CD$

Phương pháp giải

Sử dụng mối liên hệ giữa cung và dây

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

+) Cung lớn hơn căng dây lớn hơn.

+) Dây lớn hơn căng cung lớn hơn.

+) Hai cung bằng nhau căng hai dây bằng nhau và ngược lại

Sử dụng định lý: Trong một đường tròn, đường kính là dây có độ dài lớn nhất

Lời giải của GV Loigiaihay.com

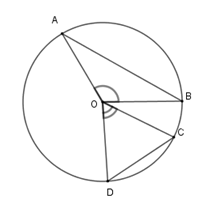
Vì $\widehat {COD} < \widehat {AOB}$ nên cung $CD$ nhỏ hơn cung $AB$, từ đó dây $CD < AB$ (*)

Xét tam giác $OCD$ cân tại $O$ có $\widehat {COD} = 60^\circ $ nên $\Delta COD$ là tam giác đều $ \Rightarrow CD = R$

$AB$ là dây không đi qua tâm nên $AB < 2R \Rightarrow AB < 2CD$ (**)

Từ (*) và (**) ta có $CD < AB < 2CD$

Đáp án : D