Một quả bóng bàn được thả rơi tự do. Quãng đường chyển động \(s\) của nó được biểu diễn gần đúng bởi công thức \(s = 3{t^2},\) với \(t\) là thời gian tính bằng giây, \(s\) tính bằng mét. Quả bóng bàn đó được thả tự do từ độ cao \(108m.\) Thời gian quả bóng bàn đó tiếp đất là:
-
A.
\(7s\)
-
B.
\(4s\)
-
C.
\(5s\)
-
D.
\(6s\)
Khi quả bóng bàn tiếp đất thì ta có \(s = 108m.\) Từ đó ta tìm được \(t.\)
Khi quả bóng bàn tiếp đất thì ta có \(s = 108m.\)
Thay vào công thức \(s = 3{t^2}\), ta được:
\( 3{t^2} = 108 \\ {t^2} = 36 \\ t = 6\,\left( s \right)\,\,\,\,\,\,\left( {do\,\,\,t > 0} \right).\)
Đáp án : D

Các bài tập cùng chuyên đề
Bài 1 :
Giá trị của hàm số $y = f\left( x \right) = - 7{x^2}$ tại ${x_0} = - 2$ là
-
A.
$28$
-
B.
$14$
-
C.
$21$
-
D.
$ - 28$
Bài 2 :
Cho hàm số \(y = f\left( x \right) = - 2{x^2}\) . Tổng các giá trị của $a$ thỏa mãn $f\left( a \right) = - 8 + 4\sqrt 3 $ là
-
A.
$1$
-
B.
$0$
-
C.
$10$
-
D.
$-10$
Bài 3 :
Giá trị của hàm số \(y = f\left( x \right) = \dfrac{4}{5}{x^2}\) tại \({x_0} = - 5\) là
-
A.
\(20\)
-
B.
\(10\)
-
C.
\(4\)
-
D.
\( - 20\)
Bài 4 :
Cho hàm số \(y = f\left( x \right) = \dfrac{1}{2}{x^2}\) . Tổng các giá trị của \(a\) thỏa mãn \(f\left( a \right) = 3 + \sqrt 5 \) là
-
A.
\(1\)
-
B.
\(2\sqrt 5 \)
-
C.
\(0\)
-
D.
\( - 2\)
Bài 5 :
Giá trị của hàm số \(y = 2{x^2}\) tại \(x = 3\) là
-
A.
\(9\)
-
B.
\(12\)
-
C.
\(18\)
-
D.
\(6\)
Bài 6 :
Lực \(F\) của gió thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương vận tốc \(v\) của gió tức là: \(F = a{v^2}\) với \(a\) là hằng số. Biết rằng khi vận tốc của gió là \(2,5m/s\) thì lực tác động lên cánh buồm là \(150N.\) Biết thuyền buồm vẫn có thể đi được nếu vận tốc gió lớn nhất là \(90km/h.\) Tính áp lực lớn nhất mà cánh buồm có thể chịu được.
-
A.
\(15000N\)
-
B.
\(12000N\)
-
C.
\(13500N\)
-
D.
\(14000N\)
Bài 7 :
Cho biết quãng đường đi được của một chiếc xe khách được xác định bởi hàm số: \(S = 54t + 2{t^2}\) ( trong đó S là quãng đường đi được tính bằng đơn vị km, t là thời gian xe chuyển động tính bằng đơn vị giờ). Giả sử lúc 9h sáng xe đang ở bến xe Miền Đông. Hỏi lúc 1h15phút chiều khoảng cách từ xe khách đến bến xe Miền Đông là bao nhiêu? (cho rằng xe khách đi thẳng từ bến xe Miền Đông đi quốc lộ 13 và xe đi không nghỉ)
-
A.
285,425km
-
B.
265,425km
-
C.
265,625km
-
D.
285,625km
Bài 8 :
Cho hàm số \(y=f\left( x \right)=a{{x}^{2}}\) có đồ thị \(\left( P \right)\) đi qua \(A\left( -3;\dfrac{9}{4} \right)\). Tính \(x\) nếu \(f\left( x \right)=8\).
-
A.
\(x = 2;x = - 2\)
-
B.
\(x = 4\sqrt 2;x = - 4\sqrt 2\)
-
C.
\(x = 4;x = - 4\)
-
D.
\(x = 2\sqrt 2;x = - 2\sqrt 2\)
Bài 9 :
Trên một hệ trục toạ độ, vẽ parabol \(\left( P \right)\) có đỉnh \(O\) và đi qua \(A\left( \sqrt{3};-3 \right)\). Hoành độ điểm thuộc \(\left( P \right)\) có tung độ bằng \(-2\) là:
-
A.
\(x = \sqrt 2;x = - \sqrt 2\)
-
B.
\(x = \sqrt 3 ; x = - \sqrt 3 \)
-
C.
\(x = 1;x = - 1\)
-
D.
\(x = 2;x = - 2\)
Bài 10 :
Cho hình chóp tứ giác đều có đáy là hình vuông cạnh a (cm) và chiều cao 15 cm.
a) Viết công thức thể tích V của hình chóp theo a và tính giá trị của V khi a = 5cm.
b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình chóp thay đổi như thế nào?
Bài 11 :
Cho hình chóp tam giác đều có đáy là tam giác đều cạnh a (cm) và chiều cao 10 cm.
a) Tính diện tích đáy S của hình chóp theo a.
b) Từ kết quả câu a, tính thể tích V của hình chóp theo a và tính giá trị của V khi a = 4 cm.
c) Nếu độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp thay đổi như thế nào?
Bài 12 :
Diện tích S của hình tròn được tính bởi công thức \(S = \pi {R^2}\).
Trong đó R là bán kính của hình tròn và \(\pi \approx 3,14.\)
a) Tính diện tích của hình tròn với R = 10 cm.
b) Diện tích S có phải là hàm số của biến số R không?
Bài 13 :
a) Xác định hệ số của x2 trong các hàm số sau: y = 0,75x2 ; y = - 3x2 ; \(y = \frac{1}{4}{x^2}\)
b) Với mỗi hàm số đã cho ở câu a), tính giá trị của y khi x = - 2; x = 2.
Bài 14 :
Gọi x (cm) là chiều dài cạnh của một viên gạch lát nền hình vuông.
a) Viết công thức tính diện tích S (cm2) của viên gạch đó.
b) Tính S khi x = 20; x = 30; x = 60.
Bài 15 :
Cho hàm số \(y = 2{x^2}\). Khi y = 2 thì
A. x = 1
B. x = 2 hoặc x = - 2
C. x = 1 hoặc x = - 1
D. x = 2
Bài 16 :
Xét hàm số \(y = 5{x^2}\) trong tình huống mở đầu.
Hàm số có dạng \(y = a{x^2}(a \ne 0)\) hay không? Nếu có, hãy xác định hệ số a của \({x^2}\).
Bài 17 :
Hàm số nào sau đây có dạng \(y = a{x^2}(a \ne 0)\)? Đối với những hàm số đó, xác định hệ số a của \({x^2}\).
a) \(y = - {x^2}\)
b) \(y = \frac{{{x^2}}}{2}\)
c) \(y = \frac{1}{{4{x^2}}}\)
Bài 18 :
Cho hàm số \(y = \frac{2}{3}{x^2}\). Hãy tính giá trị của y khi:
a) \(x = - 3\)
b) \(x = 0\)
c) \(x = 3\)
Bài 19 :
Cho hàm số \(y = a{x^2}\). Tìm a, biết rằng khi \(x = - 3\) thì \(y = 5\).
Bài 20 :
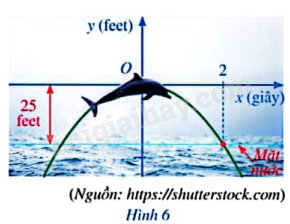
Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol \(y = a{x^2}\), với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. tìm hàm số biểu thị quỹ đạo nhảy của cá heo.
Bài 21 :
Viết hàm số biểu thị diện tích S (cm2) của tam giác vuông cân có độ dài cạnh góc vuông bằng x (cm). Tính S khi x lần lượt bằng 2 cm, 2,5 cm, 6 cm.
Bài 22 :
Một vật rơi ở độ cao 80 m sao với mặt đất. Quãng đường chuyển động s (m) của vật rơi phụ thuộc vào thời gian t (s) bởi công thức s = 5t2.
a) Tính quãng đường chuyển động của vật sau 2 giây.
b) Hỏi sau bao lâu vật này tiếp đất?
Bài 23 :
Viết hàm số biểu thị diện tích S (cm2) của tam giác đều có cạnh bằng a (cm). Tính S khi a lần lượt bằng 2 cm; 4 cm; 5 cm.
Bài 24 :
Động năng Wđ (đơn vị : Jun, kí hiệu: J) của một vật có khối lượng m (kg) là năng lượng mà vật đó có được khi chuyển động với tốc độ v (m/s) và được tính theo công thức Wđ \( = \frac{1}{2}m{v^2}\). Cho biết khi vật chuyển động với tốc độ 4 m/s thì động năng sinh ra là 16 J, hãy xác định động năng của vật đó khi nó di chuyển với tốc độ 5 m/s.
Bài 25 :
Nhiệt lượng toả ra Q(J) trong 1 giây trên một đoạn dây dẫn khi có dòng điện với cường độ I(A) chạy qua được tính theo công thức Q = aI2. Biết khi I = 2 (A) thì Q = 3,4 (J). Hãy xác định Q khi I lần lượt bằng 0,5 A; 1 A; 1,2 A.
Bài 26 :
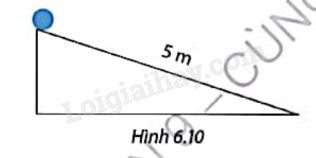
Một viên bi lăn từ vị trí cao nhất của một mặt phẳng nghiêng dài 5 m (Hình 6.10). Quãng đường s (m) viên bi lăn được sau t (s) kể từ khi bắt đầu chuyển động được cho bởi công thức s = 0,05t2 . Tính thời gian viên bi lăn hết chiều dài mặt phẳng nghiêng.
Bài 27 :
Cho hàm số f(x) = -3x2. Khẳng định nào sau đây đúng?
A. f(-1) = 3.
B. f(-2) = 12.
C. f(-3) = -27
D. f(-4) = -24
Bài 28 :
Thể tích V của hình lăng trụ đứng tứ giác có đáy là hình vuông và chiều cao 5cm là một hàm số của độ dài cạnh đáy a (cm).
a) Viết công thức của hàm số này và tính độ dài cạnh đáy của hình lăng trụ nếu biết thể tích bằng \(180c{m^3}\).
b) Nếu độ dài cạnh a của hình vuông đáy tăng lên hai lần thì thể tích V của khối lăng trụ thay đổi như thế nào?
Bài 29 :
Một bể nước dạng hình hộp chữ nhật với đáy là hình vuông có độ dài cạnh là x (m). Chiều cao của bể bằng 1,5 m. Gọi V là thể tích của bể.
a) Viết công thức tính thể tích V (m3) theo x.
b) Giả sử chiều cao của bể không đổi. Tính thể tích của bể khi x lần lượt nhận các giá trị: 1; 2; 3. Khi x tăng lên 2 lần, 3 lần thì thể tích của bể tăng lên mấy lần?
Bài 30 :
Cho hàm số \(y = {\rm{a}}{{\rm{x}}^2}\)\(\left( {a \ne 0} \right)\), biết \(\left( { - 1;2} \right)\) là một cặp giá trị tương ứng của hàm số. Vậy hệ số \(a\) bằng:


















Danh sách bình luận