Đề bài

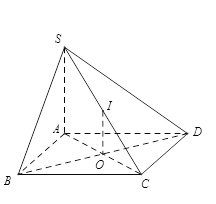
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và đáy \(ABCD\) là hình chữ nhật. Gọi \(O\) là tâm của \(ABCD\) và \(I\) là trung điểm của \(SC\). Khẳng định nào sau đây sai ?

• A. \(IO \bot \left( {ABCD} \right).\)
• B. \(BC \bot SB.\)
• C. \(\left( {SAC} \right)\) là mặt phẳng trung trực của đoạn \(BD.\)
• D. Tam giác \(SCD\) vuông ở \(D.\)

Phương pháp giải

Sử dụng điều kiện đường thẳng vuông góc mặt phẳng và định nghĩa mặt phẳng trung trực để xét tính đúng, sai của từng đáp án.

Lời giải của GV Loigiaihay.com

Có \(IO\)   là đường trung bình tam giác \(SAC\)   nên \(IO//SA\)   nên \(IO \bot \left( {ABCD} \right)\)  nên A đúng.

Có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot SB\)  nên B đúng

Và \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot SD\) nên phương án D đúng.

Đáp án C sai vì nếu \(\left( {SAC} \right)\) là mặt phẳng trung trực của \(BD\) \( \Rightarrow BD \bot AC\)(vô lý).

Đáp án : C