Đề bài

Cho tam giác $ABC$ cân tại $A$ , đường cao $AH = 2cm,BC = 8cm$ . Đường vuông góc với $AC$ tại $C$ cắt đường thẳng $AH$ ở $D$ .

Câu 1

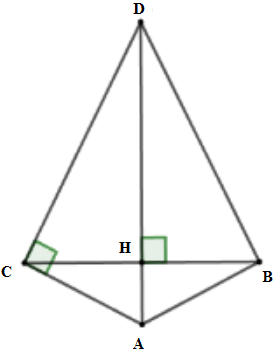
Các điểm nào sau đây cùng thuộc một đường tròn?

A.

$D,H,B,C$

B.

$A,B,H,C$

C.

$A,B,D,H$

D.

$A,B,D,C$

Đáp án : D

Phương pháp giải

Xác định điểm cách đều cả bốn đỉnh  cho trước. 

Lời giải của GV Loigiaihay.com

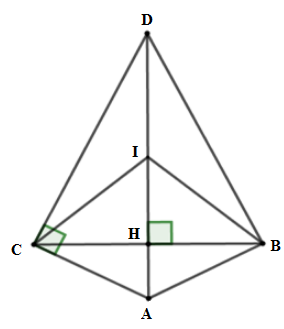
Ta có $\Delta ABC$ cân tại $A$ có đường cao $AH$ nên $AH$ cũng là đường phân giác $ \Rightarrow \widehat {CAD} = \widehat {DAB}$

Suy ra $\Delta ACD = \Delta ABD\left( {c - g - c} \right)$ nên $\widehat {ABD} = \widehat {ACD} = 90^\circ $.

Lấy $I$ là trung điểm $AD$. Xét hai tam giác vuông $ABD$ và $ACD$ có $IA = ID = IB = IC = \dfrac{{AD}}{2}$

Nên $I$ là điểm cách đều $A,B,D,C$ hay $A,B,D,C$ cùng nằm trên dường tròn tâm $I$ đường kính $AD$.

---

Xem thêm các câu hỏi cùng đoạn

Câu 2

Tính đường kính của đường tròn đi qua các điểm $A, B, D, C.$

A.

$d = 8\,cm$

B.

$d = 12\,cm$

C.

$d = 10\,cm$

D.

$d = 5\,cm$

Đáp án : C

Phương pháp giải

Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông.

Lời giải của GV Loigiaihay.com

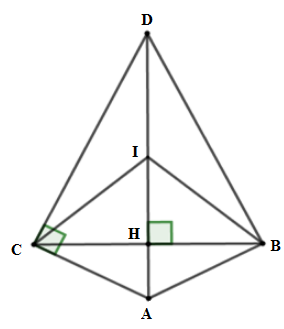
Từ câu trước ta có bốn điểm $A,B,D,C$ cùng thuộc đường tròn đường kính $AD$ suy ra ta cần tính độ dài $AD$.

Vì $BC = 8\,cm \Rightarrow BH = 4\,cm$. Áp dụng định lý Pytago cho tam giác vuông $AHB$ ta được $AB = \sqrt {A{H^2} + B{H^2}}  = \sqrt {4 + 16}  = 2\sqrt 5 $

Áp dụng hệ thức lượng trong tam giác vuông $ABD$ ta có $A{B^2} = AH.AD$$\Rightarrow AD = \dfrac{{A{B^2}}}{{AH}} = \dfrac{{20}}{2} = 10$

Vậy đường kính cần tìm là $10\,cm$.

---