Đề bài

Cho hình lập phương \(ABCD.A'B'C'D'\). Chọn khẳng định sai?

• A. Góc giữa $AC$ và \(B'D'\) bằng $90^\circ $.
• B. Góc giữa \(B'D'\) và \(AA'\) bằng $60^\circ $.
• C. Góc giữa $AD$ và \(B'C\) bằng $45^\circ $.
• D. Góc giữa $BD$ và \(A'C'\) bằng $90^\circ $.

Phương pháp giải

Xác định góc giữa các đường thẳng và kết luận (sử dụng tích vô hướng của hai véc tơ).

Lời giải của GV Loigiaihay.com

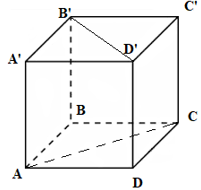
Ta có: $\overrightarrow {AA'} .\overrightarrow {B'D'}  = \overrightarrow {BB'} .\overrightarrow {BD}  = \overrightarrow {BB'} .\left( {\overrightarrow {BA}  + \overrightarrow {BC} } \right)$ $ = \overrightarrow {BB'} .\overrightarrow {BA}  + \overrightarrow {BB'} .\overrightarrow {BC}  = 0$

(vì $\left( {\overrightarrow {BB'} ,\overrightarrow {BA} } \right) = {90^0}$ và $\left( {\overrightarrow {BB'} ,\overrightarrow {BC} } \right) = {90^0}$)

Do đó: $\left( {\overrightarrow {AA'} ,\overrightarrow {B'D'} } \right) = {90^0} \Rightarrow \widehat {\left( {AA',B'D'} \right)} = {90^0}$

Đáp án : B