Đề bài

Cho tứ diện $ABCD$ có $AB = AC = AD$ và \(\widehat {BAC} = \widehat {BAD} = {60^0}\). Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {IJ} \) và \(\overrightarrow {CD} \)?

• A. $45^\circ $
• B. $90^\circ $
• C. $60^\circ $
• D. $120^\circ $

Phương pháp giải

Sử dụng các tính chất của tam giác đều, tam giác cân

Lời giải của GV Loigiaihay.com

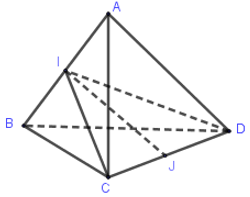
Ta có $BAC$ và $BAD$ là 2 tam giác đều, $I$ là trung điểm của $AB$ nên $CI = DI$ (2 đường trung tuyến của 2 tam giác đều chung cạnh $AB$) nên $CID$ là tam giác cân ở $I$. Do đó $IJ \bot CD$

Đáp án : B