Đề bài

Cho tứ diện \(ABCD.\) \(M\) là điểm trên đoạn \(AB\) và \(MB = 2MA\). \(N\) là điểm trên đường thẳng $CD$ mà \(\overrightarrow {CN}  = k\overrightarrow {CD} \). Nếu  \(\overrightarrow {MN} ,\overrightarrow {AD} ,\overrightarrow {BC} \) đồng phẳng thì giá trị của \(k\) là:

• A. \(k = \dfrac{2}{3}\).
• B. \(k = \dfrac{3}{2}\). 
• C. \(k = \dfrac{4}{3}\). 
• D. \(k = \dfrac{1}{2}\).

Phương pháp giải

- Dựng mặt phẳng \(\left( \alpha  \right)\) đi qua \(M\) và song song với cả hai đường thẳng \(BC\) và \(AD\) cắt \(CD\) tại \(N\).

- Chứng minh ba véc tơ \(\overrightarrow {MN} ,\overrightarrow {AD} ,\overrightarrow {BC} \) đồng phẳng.

- Tính tỉ số \(\dfrac{{CN}}{{CD}}\)  và suy ra đáp số.

Lời giải của GV Loigiaihay.com

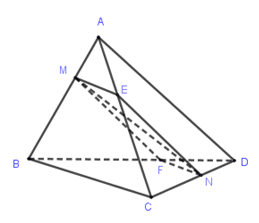
Qua \(M\) vẽ mặt phẳng \(\left( \alpha  \right)\) song song với \(AD\) và \(BC\).

\(\left( \alpha  \right)\)cắt \(AC\) tại \(E\), \(BD\) tại \(F\) và \(CD\) tại \(N\). Ta có \(MF{\rm{//}}EN{\rm{//}}AD\).

Các vecto \(\overrightarrow {MN} ,\overrightarrow {AD} ,\overrightarrow {BC} \) có giá song song hay nằm trong mặt phẳng \(\left( \alpha  \right)\) nên đồng phẳng.

Ta có: \(\dfrac{{CN}}{{CD}} = \dfrac{{BF}}{{BD}} = \dfrac{{BM}}{{BA}} = \dfrac{2}{3}\)(Ta – let) nên \(\overrightarrow {CN}  = \dfrac{2}{3}\overrightarrow {CD} \).

Vậy \(k = \dfrac{2}{3}\).

Đáp án : A