Đề bài

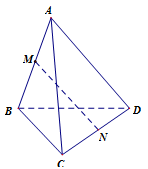
Cho tứ diện \(ABCD\), \(M\) và \(N\) theo thứ tự là trung điểm của \(AB\) và \(CD\). Bộ ba vecto nào dưới đây đồng phẳng?

• A. \(\overrightarrow {BC} ,\overrightarrow {BD} ,\overrightarrow {AD} .\)   
• B. \(\overrightarrow {AC} ;\overrightarrow {AD} ;\overrightarrow {MN} .\) 
• C. $\overrightarrow {BC} ;\overrightarrow {AD} ;\overrightarrow {MN} .$ 
• D. \(\overrightarrow {AC} ;\overrightarrow {DC} ;\overrightarrow {MA} .\) 

Phương pháp giải

Ba véc tơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng \( \Leftrightarrow \exists m,n\) sao cho \(\overrightarrow c  = m.\overrightarrow a  + n.\overrightarrow b \) (.$m,n$. là duy nhất).

Lời giải của GV Loigiaihay.com

\(\begin{array}{l}\overrightarrow {AD}  = \overrightarrow {AM}  + \overrightarrow {MN}  + \overrightarrow {ND} \\\overrightarrow {BC}  = \overrightarrow {BM}  + \overrightarrow {MN}  + \overrightarrow {NC} \\ \Rightarrow \overrightarrow {AD}  + \overrightarrow {BC}  = 2\overrightarrow {MN}  \Rightarrow \overrightarrow {MN}  = \dfrac{1}{2}\overrightarrow {AD}  + \dfrac{1}{2}\overrightarrow {BC} \end{array}\)

Vậy ba vecto $\overrightarrow {BC} ;\overrightarrow {AD} ;\overrightarrow {MN} $ đồng phẳng.

Đáp án : C