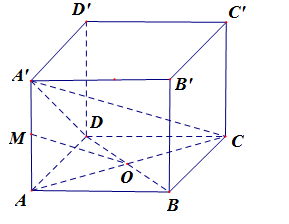
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(M\) là trung điểm của \(AA'\), \(O\) là tâm của hình bình hành \(ABCD\). Cặp ba vecto nào sau đây đồng phẳng?
-
A.
\(\overrightarrow {MO} ,\overrightarrow {AB} \) và \(\overrightarrow {B'C} \)
-
B.
\(\overrightarrow {MO} ,\overrightarrow {AB} \) và \(\overrightarrow {A'D'} \) .
-
C.
\(\overrightarrow {MO} ,\overrightarrow {DC'} \) và $\overrightarrow {B'C} $
-
D.
$\overrightarrow {MO} ,\overrightarrow {A'D} $ và \(\overrightarrow {B'C'} \).
Kiểm tra tính đồng phẳng của các véc tơ bằng cách tìm một mặt phẳng song song với giá của cả ba véc tơ, nếu ta chỉ ra được mặt phẳng đó thì ba véc tơ đồng phẳng.
Ta có \(MO{\rm{//}}\left( {CDA'B'} \right);\)
\(AB//A'B' \Rightarrow AB{\rm{//}}\left( {CDA'B'} \right),\)
\(B'C\) nằm trong mặt phẳng \(\left( {CDA'B'} \right)\) nên các vecto \(\overrightarrow {MO} ,\overrightarrow {AB} ,\overrightarrow {B'C} \) dồng phẳng vì có giá song song hay nằm trên mặt phẳng \(\left( {CDA'B'} \right)\).
Đáp án : A
Ta có thể giải bài toán bằng cách khác như sau:
Ta có \(\overrightarrow {MO} = \dfrac{1}{2}\overrightarrow {A'C} = \dfrac{1}{2}\left( {\overrightarrow {A'B'} + \overrightarrow {B'C} } \right) = \dfrac{1}{2}\left( {\overrightarrow {A'B'} + \overrightarrow {B'C'} } \right) = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {B'C} \)
Vậy các vecto \(\overrightarrow {MO} ,\overrightarrow {AB} ,\overrightarrow {BC} \) đồng phẳng.

Các bài tập cùng chuyên đề

















