Đề bài

Cho hình vẽ, MA và MB là hai tiếp tuyến của đường tròn \(\left( {O,3cm} \right)\), \(MA = 4cm\). Độ dài đoạn thẳng AB là:

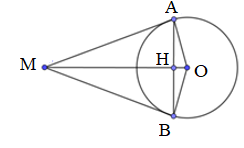
• A. 4,8cm
• B. 2,4cm
• C. 1,2cm 
• D. 9,6cm

Phương pháp giải

Áp dụng hệ thức lượng trong tam giác vuông.

Lời giải của GV Loigiaihay.com

Vì MA và MB  là tiếp tuyến nên \(MA = MB\) nên M  thuộc trung trực của AB

Mà \(OA = OB\) do cùng là bán kính nên O  thuộc trung trực của AB

Suy ra OM  là trung trực của AB. Gọi H  là giao điểm của MO và AB, ta có \(AH = BH\)

Xét tam giác vuông AMO vuông tại A (do MA là tiếp tuyến) có AH  là đường cao

\( \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{{A{O^2}}} \Rightarrow AH = \sqrt {\dfrac{{A{M^2}.A{O^2}}}{{A{M^2} + A{O^2}}}}  = \sqrt {\dfrac{{{4^2}{{.3}^2}}}{{{4^2} + {3^2}}}}  = 2,4\)

Suy ra \(AB = 2AH = 2.2,4 = 4,8\).

Đáp án : A