Đề bài

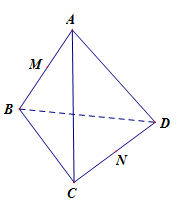
Cho tứ diện đều \(ABCD\),\(M\) và \(N\) theo thứ tự là trung điểm của cạnh \(AB\) và \(CD\). Mệnh đề nào sau đây sai?

• A. \(\overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {AD}  + \overrightarrow {BC} \) 
• B. \(\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right)\)
• C. \(\overrightarrow {AC}  + \overrightarrow {BD}  + \overrightarrow {AD}  + \overrightarrow {BC}  =  - 4\overrightarrow {NM} \).
• D. \(\overrightarrow {MC}  + \overrightarrow {MD}  - 4\overrightarrow {MN}  = \overrightarrow 0 \).

Phương pháp giải

Xét tính đúng, sai của từng đáp án dựa vào công thức trung điểm và các công thức cộng, trừ véc tơ.

Lời giải của GV Loigiaihay.com

A.Đúng vì:  \(\overrightarrow {AC}  + \overrightarrow {BD}  = \left( {\overrightarrow {AD}  + \overrightarrow {DC} } \right) + \left( {\overrightarrow {BC}  + \overrightarrow {CD} } \right) = \overrightarrow {AD}  + \overrightarrow {BC} \)

B. Đúng vì: \(\overrightarrow {AD}  + \overrightarrow {BC}  = \left( {\overrightarrow {AM}  + \overrightarrow {MN}  + \overrightarrow {ND} } \right) + \left( {\overrightarrow {BM}  + \overrightarrow {MN}  + \overrightarrow {NC} } \right)\)\( = 2\overrightarrow {MN}  + \left( {\overrightarrow {AM}  + \overrightarrow {BM} } \right) + \left( {\overrightarrow {ND}  + \overrightarrow {NC} } \right) = 2\overrightarrow {MN} \)

C.Đúng vì:  \(\overrightarrow {AC}  + \overrightarrow {BD}  + \overrightarrow {AD}  + \overrightarrow {BC}  = 2\overrightarrow {AN}  + 2\overrightarrow {BN}  = 2\left( {\overrightarrow {AN}  + \overrightarrow {BN} } \right) =  - 2\left( {\overrightarrow {NA}  + \overrightarrow {NB} } \right) =  - 4\overrightarrow {NM} \)

Vậy D sai.

Đáp án : D