Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Từ tỉ số lượng giác sin, cos để chứng minh.
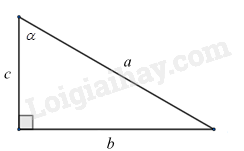
Giả sử ta có tam giác vuông có các cạnh và góc $\alpha $ như hình vẽ.
Áp dụng tỉ số lượng giác của góc nhọn, ta có:
$\sin \alpha =\frac{b}{a},\cos \alpha =\frac{c}{a},\tan \alpha =\frac{b}{c},\cot \alpha =\frac{c}{b}$.
Ta có: ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha ={{\left( \frac{b}{a} \right)}^{2}}+{{\left( \frac{c}{a} \right)}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}}{{{a}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}}=1$
Vậy ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
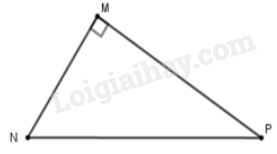
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Bài 2 :
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.
-
A.
$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\,\,$
-
B.
$\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}\,\,$
-
C.
$\tan \alpha .\cot \alpha = 1$
-
D.
${\tan ^2}\alpha - 1 = {\cos ^2}\alpha $
Bài 3 :
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
-
A.
$\sin B = 0,6;\cos B = 0,8$
-
B.
$\sin B = 0,8;\cos B = 0,6$
-
C.
$\sin B = 0,4;\cos B = 0,8$
-
D.
$\sin B = 0,6;\cos B = 0,4$
Bài 4 :
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
Bài 5 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\cos C \approx 0,76$
-
B.
$\cos C \approx 0,77$
-
C.
$\cos C \approx 0,75$
-
D.
$\cos C \approx 0,78$
Bài 6 :
Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha = \dfrac{2}{5}\).
-
A.
$\sin \alpha = \dfrac{{\sqrt {21} }}{{25}};\cot \alpha = \dfrac{{3\sqrt {21} }}{{21}}$
-
B.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{5}{{\sqrt {21} }}$
-
C.
$\sin \alpha = \dfrac{{\sqrt {21} }}{3};\cot \alpha = \dfrac{3}{{\sqrt {21} }}$
-
D.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{2}{{\sqrt {21} }}$
Bài 7 :
Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha + {\cos ^4}\alpha $ bằng
-
A.
$C = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $
-
B.
$C = 1$
-
C.
$C = {\sin ^2}\alpha .{\cos ^2}\alpha $
-
D.
$C = 1 + 2{\sin ^2}\alpha .{\cos ^2}\alpha $
Bài 8 :
Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $ ta được
-
A.
$P = {\sin ^2}\alpha $
-
B.
$P = {\cos ^2}\alpha $
-
C.
$P = {\tan ^2}\alpha $
-
D.
$P = 2{\sin ^2}\alpha $
Bài 9 :
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
-
A.
$Q = 1 + {\tan ^2}\alpha $
-
B.
$Q = 1 + 2{\tan ^2}\alpha $
-
C.
$Q = 1 - 2{\tan ^2}\alpha $
-
D.
$Q = 2{\tan ^2}\alpha $
Bài 10 :
Cho $\tan \alpha = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}$
-
A.
$G =1$
-
B.
$G = - \dfrac{4}{5}$
-
C.
$G = - \dfrac{6}{5}$
-
D.
$G = - 1$
Bài 11 :
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$2$
-
B.
$3$
-
C.
$1$
-
D.
$4$
Bài 12 :
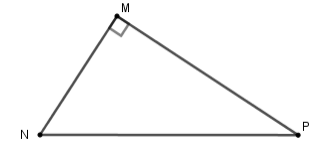
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
-
A.
\(\dfrac{{MN}}{{NP}}\)
-
B.
\(\dfrac{{MP}}{{NP}}\)
-
C.
\(\dfrac{{MN}}{{MP}}\)
-
D.
\(\dfrac{{MP}}{{MN}}\)
Bài 13 :
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
Bài 14 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
-
A.
\(\tan C \approx 0,67\)
-
B.
\(\tan C \approx 0,5\)
-
C.
\(\tan C \approx 1,4\)
-
D.
\(\tan C \approx 1,5\)
Bài 15 :
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(CH = 11\,cm,\,BH = 12\,cm.\) Tính tỉ số lượng giác \(\cos C\) (làm tròn đến chữ số thập phân thứ \(2\) )
-
A.
\(\cos C \approx 0,79\)
-
B.
\(\cos C \approx 0,69\)
-
C.
\(\cos C \approx 0,96\)
-
D.
\(\cos C \approx 0,66\)
Bài 16 :
Tính \(\sin \alpha ,\,\,\tan \alpha \) biết \(\cos \alpha = \dfrac{3}{4}\).
-
A.
\(\sin \alpha = \dfrac{4}{{\sqrt 7 }};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
B.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{3}{{\sqrt 7 }}\)
-
C.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
D.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{3};\tan \alpha = \dfrac{{\sqrt 7 }}{4}\)
Bài 17 :
Cho \(\alpha \) là góc nhọn bất kỳ. Khi đó \(C={\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha {\cos ^2}\alpha \) bằng
-
A.
\(C = 1 - 3{\sin ^2}\alpha .{\cos ^2}\alpha \)
-
B.
$C=1$
-
C.
\(C = {\sin ^2}\alpha .{\cos ^2}\alpha \)
-
D.
\(C = 3{\sin ^2}\alpha .{\cos ^2}\alpha - 1\)
Bài 18 :
Cho \(\alpha \) là góc nhọn bất kỳ. Cho \(P = \left( {1 - {{\sin }^2}\alpha } \right).{\tan ^2}\alpha + \left( {1 - {{\cos }^2}\alpha } \right){\cot ^2}\alpha \), chọn kết luận đúng.
-
A.
\(P > 1\)
-
B.
\(P < 1\)
-
C.
\(P = 1\)
-
D.
\(P = 2{\sin ^2}\alpha \)
Bài 19 :
Cho \(\alpha \) là góc nhọn bất kỳ. Biểu thức \(Q = \dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\cos \alpha .\sin \alpha }}\) bằng
-
A.
\(Q = \cot \alpha - \tan \alpha \)
-
B.
\(Q = \cot \alpha + \tan \alpha \)
-
C.
\(Q = \tan \alpha - \cot \alpha \)
-
D.
\(Q = 2\tan \alpha \)
Bài 20 :
Cho \(\tan \alpha = 4\). Tính giá trị của biểu thức \(P = \dfrac{{3\sin \alpha - 5\cos \alpha }}{{4\cos \alpha + \sin \alpha }}\)
-
A.
\(P = \dfrac{7}{8}\)
-
B.
\(P = \dfrac{{17}}{8}\)
-
C.
\(P = \dfrac{8}{7}\)
-
D.
\(P = \dfrac{5}{8}\)
Bài 21 :
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 3:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$3$
-
B.
$5$
-
C.
\(\dfrac{3}{5}\)
-
D.
\(\dfrac{5}{3}\)
Bài 22 :
Chọn kết luận đúng về giá trị biểu thức \(B = \dfrac{{{{\cos }^2}\alpha - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}\) biết \(\tan \alpha = 3.\)
-
A.
\(B > 0\)
-
B.
\(B < 0\)
-
C.
\(0 < B < 1\)
-
D.
\(B = 1\)
Bài 23 :
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
-
A.
\(\sin A = \dfrac{{120}}{{169}}\)
-
B.
\(\sin A = \dfrac{{60}}{{169}}\)
-
C.
\(\sin A = \dfrac{5}{6}\)
-
D.
\(\sin A = \dfrac{{10}}{{13}}\)
Bài 24 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{3}{5}\)
-
C.
\(\dfrac{4}{3}\)
-
D.
\(\dfrac{4}{5}\)
Bài 25 :
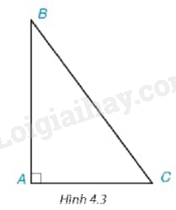
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Bài 26 :
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B'} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A'B'C';\)
b) \(\frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Bài 27 :
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Bài 28 :
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.
Bài 29 :
Trong Hình 4.32, \(\cos \alpha \) bằng
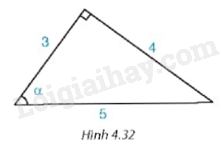
A. \(\frac{5}{3}.\)
B. \(\frac{3}{4}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{4}{5}.\)
Bài 30 :
Trong tam giác MNP vuông tại M (H.4.33), \(\sin \widehat {MNP}\) bằng:
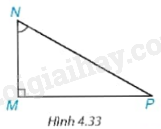
A. \(\frac{{PN}}{{MN}}\)
B. \(\frac{{MP}}{{PN}}\)
C. \(\frac{{MN}}{{PN}}\)
D. \(\frac{{MN}}{{MP}}\)


















Danh sách bình luận