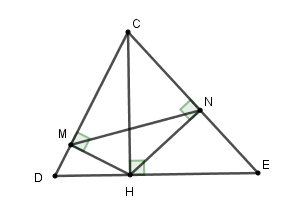
Cho tam giác $CDE$ nhọn, đường cao $CH.$ Gọi $M,N$ theo thứ tự là hình chiếu của $H$ lên $CD,CE.$ (hình vẽ)
Tích $CD.CM$ bằng
Tích $CD.CM$ bằng
\(CH.CE\)
\(CE.CN\)
\(CH.CN\)
\(CD.CN\)
Đáp án : B
Tam giác $CHD$ vuông tại $H$, ta có $C{H^2} = CM.CD$
Tam giác $CHE$ vuông tại $H$, ta có $C{H^2} = CN.CE$
Nên $CM.CD = CN.CE$.

Tam giác $CMN$ đồng dạng với tam giác nào dưới đây?
Tam giác $CMN$ đồng dạng với tam giác nào dưới đây?
\(\Delta CED\)
\(\Delta HMN\)
\(\Delta CHD\)
\(\Delta CNH\)
Đáp án : A
Chứng minh tam giác đồng dạng bằng cách sử dụng trường hợp đồng dạng thứ hai cạnh-góc-cạnh
Từ câu trước ta có $CM.CD = CN.CE $$\Leftrightarrow \dfrac{{CM}}{{CN}} = \dfrac{{CE}}{{CD}}$
Xét $\Delta CMN$ và $\Delta CED$ có $\widehat C$ chung và $\dfrac{{CM}}{{CN}} = \dfrac{{CE}}{{CD}}$ nên $\Delta CMN\backsim\Delta CED\,\,\left( {c - g - c} \right)$

Các bài tập cùng chuyên đề

















