Đề bài

Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB:AC = 3:4\) và \(AB + AC = 21cm\).

Câu 1

Tính các cạnh của tam giác \(ABC\).

A.

$AB = 9;AC = 10;BC = 15$

B.

$AB = 9;AC = 12;BC = 15$  

C.

$AB = 8;AC = 10;BC = 15$

D.

$AB = 8;AC = 12;BC = 15$

Đáp án : B

Phương pháp giải

Bước 1: Sử dụng tính chất tỉ lệ thức để tìm $AB,AC$. $\left( {\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}}} \right)$

 Bước 2: Tính $BC$ theo định lý Pytago

Lời giải của GV Loigiaihay.com

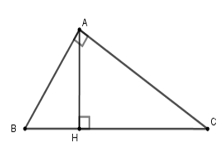
Theo giả thiết:  \(AB:AC = 3:4\),

suy ra \(\dfrac{{AB}}{3} = \dfrac{{AC}}{4} = \dfrac{{AB + AC}}{{3 + 4}} = 3\). Do đó \(AB = 3.3 = 9\)\(\left( {cm} \right)\); \(AC = 3.4 = 12\left( {cm} \right)\).

Tam giác \(ABC\) vuông tại \(A\), theo định lý Py-ta-go ta có:

\(B{C^2} = A{B^2} + A{C^2} \)\(= {9^2} + {12^2} = 225\), suy ra \(BC = 15cm\).

---

Xem thêm các câu hỏi cùng đoạn

Câu 2

Tính độ dài các đoạn \(AH,BH,CH\).

A.

$BH = 7,2;AH = 5,4;CH = 9,6$

B.

$CH = 7,2;BH = 5,4;AH = 9,6$

C.

$AH = 7,2;BH = 5,4;CH = 9$

D.

$AH = 7,2;BH = 5,4;CH = 9,6$

Đáp án : D

Phương pháp giải

Sử dụng các hệ thức giữa cạnh và đường cao trong tam giác vuông: \(A{B^2} = BH.BC\) và $AH.BC = AB.AC$

Lời giải của GV Loigiaihay.com

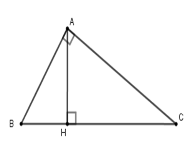
Ta có $AB = 9;AC = 12;BC = 15$

$ \Rightarrow AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}}$$ = \dfrac{{12.9}}{{15}} = 7,2$ $A{B^2} = BH.BC \Rightarrow BH $$= \dfrac{{A{B^2}}}{{BC}} $$= \dfrac{{81}}{{15}} = 5,4$

$ \Rightarrow CH = BC - BH = 15 - 5,4 = 9,6$

Vậy $AH = 7,2;BH = 5,4;CH = 9,6$.

---