Đề bài

Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 3cm,\,AC = 4cm,\,\) đường cao \(AH\) và đường trung tuyến \(AM\). Độ dài đoạn thẳng \(HM\) là

• A. \(HM = \dfrac{7}{{10}}cm\)
• B. \(HM = \dfrac{9}{5}cm\)
• C. \(HM = \dfrac{{43}}{{10}}cm\)            
• D. \(HM = \dfrac{5}{2}cm\)

Phương pháp giải

+) Sử dụng hệ thức lượng trong tam giác vuông tính \(BH\).

+) Tính \(HM = BM - BH\).

Lời giải của GV Loigiaihay.com

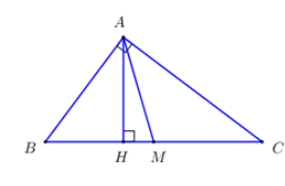
Áp dụng định lí Pytago trong tam giác vuông \(ABC:\,\,BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{3^2} + {4^2}}  = 5\,\,\left( {cm} \right)\).

Áp dụng hệ thức lượng trong tam giác vuông \(ABC:\,\,A{B^2} = BC.BH \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{9}{5}\,\,\left( {cm} \right)\).

\(M\) là trung điểm của \(BC \Rightarrow BM = \dfrac{1}{2}BC = \dfrac{5}{2}\,\,\left( {cm} \right)\).

Vậy \( \Rightarrow HM = BM - BH = \dfrac{7}{{10}}\,\,\left( {cm} \right)\)

Đáp án : A