Đề bài

Cho \(\Delta ABC\) cân tại \(A\), kẻ đường cao \(AH\) và \(CK\) . Biết \(AH = 7,5cm;\,\,\,CK = 12cm.\) Tính \(BC,AB\).

• A. \(AB = 10,5cm\,\,;\,\,\,BC = 18cm\)
• B. \(AB = 12cm\,\,;\,\,\,BC = 22cm\)
• C. \(AB = 12,5cm\,\,;\,\,\,BC = 20cm\)
• D. \(AB = 15cm\,\,;\,\,\,BC = 24cm\)

Phương pháp giải

Sử dụng định lý Pitago, hệ thức lượng trong tam giác vuông, công thức tính diện tích tam giác và tính chất tam giác cân.

Lời giải của GV Loigiaihay.com

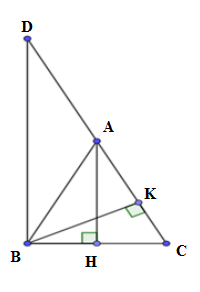
Đặt \(BH = x\,\,\,\,\left( {x > 0,\,\,\,cm} \right)\)

Ta có:  \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}CK.AB\)

\(\begin{array}{l} \Leftrightarrow AH.BC = CK.AB\\ \Leftrightarrow 7,5.2x = 12.AB \Leftrightarrow AB = \dfrac{5}{4}x\end{array}\)

Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) ta có:

\(A{B^2} = B{H^2} + A{H^2}\) \( \Leftrightarrow \dfrac{{25}}{{16}}{x^2} = {x^2} + 7,{5^2} \Leftrightarrow \dfrac{9}{{16}}{x^2} = 7,{5^2}\)\( \Leftrightarrow {x^2} = 100 \Rightarrow x = 10\)\( \Rightarrow AB = \dfrac{5}{4}.10 = 12,5\,\,cm\)

Ta có: \(\Delta ABC\) cân tại \(A \Rightarrow AH\) là đường cao đồng thời là đường trung tuyến (định lý)

\( \Rightarrow H\) là trung điểm của \(BC\)\( \Rightarrow BC = 2BH = 20cm\)

Đáp án : C