Đề bài

Cho hàm số bậc ba \(y = f\left( x \right)\) có bảng biến thiên trong hình dưới:

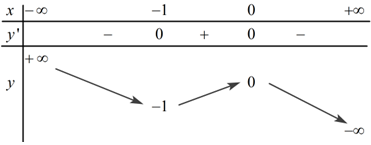
Số nghiệm của phương trình \(f\left( x \right) =  - 0,5\) là:

• A. \(2\)
• B. \(3\)
• C. \(1\)
• D. \(4\)

Phương pháp giải

Số nghiệm của phương trình \(f\left( x \right) =  - 0,5\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y =  - 0,5.\)

Dựa vào BBT để xác định số giao điểm của hai đồ thị hàm số.

Lời giải của GV Loigiaihay.com

Số nghiệm của phương trình \(f\left( x \right) =  - 0,5\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y =  - 0,5.\)

Ta có BBT:

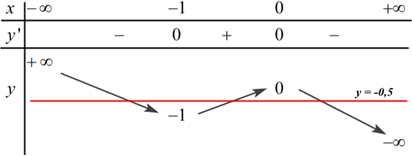
Dựa vào BBT ta thấy đường thẳng \(y =  - 0,5\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt.

\( \Rightarrow \) Phương trình \(f\left( x \right) =  - 0,5\) có \(3\) nghiệm phân biệt.

Đáp án : B