Trong thí nghiệm giao thoa sóng mặt nước giữa hai nguồn đồng bộ tần số 25Hz , cách nhau S1S2=32 cm , tốc độ truyền sóng trên mặt nước là 30 cm/s. M là điểm trên mặt nước cách đều hai nguồn S1, S2 và cách trung điểm I của S1S2 một khoảng 12 cm . Số điểm dao động cùng pha với hai nguồn nằm trong đoạn thẳng MI là
-
A.
16
-
B.
13
-
C.
4
-
D.
3
Viết phương trình dao động sóng tại điểm N bất kì nằm trên trung trực của S1S2: \({{u}_{N}}=2Ac\text{os(}\omega \text{t-}\frac{2\pi d}{\lambda }+\varphi )\)
Tính độ lệch pha giữa N và nguồn
Tìm điều kiện để N dao động cùng pha với nguồn.
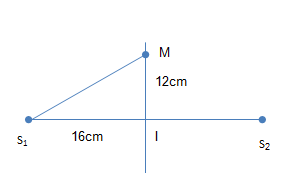
Hai nguồn đồng bộ dao động với phương trình\(u=Ac\text{os(}\omega \text{t+}\varphi )\)
Gọi điểm N cách hai nguồn khoảng d, N thuộc đoạn MI. Phương trình dao động sóng tại N:\({{u}_{N}}=2Ac\text{os(}\omega \text{t-}\frac{2\pi d}{\lambda }+\varphi )\)
Độ lệch pha giữa hai điểm N và nguồn là: \(\Delta \varphi =\frac{2\pi d}{\lambda }\)
Để N dao động cùng pha với nguồn: \(\Delta \varphi =k.2\pi \to \frac{2\pi d}{\lambda }=k.2\pi \to d=k\lambda =k.\frac{v}{f}=1,2.k(cm)\)
Vì N thuộc đoạn MI: \({{S}_{1}}I\le {{S}_{1}}N\le {{S}_{1}}M\to 16\le 1,2.k\le \sqrt{{{16}^{2}}+{{12}^{2}}}\to 13,3\le k\le 16,6\)
ð Có 3 giá trị của k
Đáp án : D
Các bài tập cùng chuyên đề
Hai nguồn sóng kết hợp trên mặt nước S1, S2 dao động với phương trình:
\({u_1} = {\rm{ }}asin(\omega t),{\rm{ }}{u_2} = {\rm{ }}acos(\omega t){\rm{ ;}}{S_1}{S_2} = {\rm{ }}9\lambda \) . Điểm M gần nhất trên trung trực của S1S2 dao động cùng pha với u1 cách S1, S2 bao nhiêu.
Hai nguồn phát sóng kết hợp S1, S2 trên mặt nước cách nhau 30 cm phát ra hai dao động điều hoà cùng phương, cùng tần số f = 50 Hz và pha ban đầu bằng không. Biết tốc độ truyền sóng trên mặt chất lỏng v = 6m/s. Những điểm nằm trên đường trung trực của đoạn S1S2 mà sóng tổng hợp tại đó luôn dao động ngược pha với sóng tổng hợp tại O ( O là trung điểm của S1S2) cách O một khoảng nhỏ nhất là:
Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp S1 và S2 cách nhau 20cm, dao động theo phương thẳng đứng với phương trình
\(u{\rm{ }} = {\rm{ }}2cos40\pi t{\rm{ }}\left( {mm} \right)\) . Biết tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. Phần tử O thuộc bề mặt chất lỏng là trung điểm của S1S2. Điểm trên mặt chất lỏng thuộc trung trực của S1S2 dao động cùng pha với O, gần O nhất, cách O đoạn:
Hai nguồn sóng kết hợp, đặt tại A và B cách nhau 20 cm dao động theo phương trình \(u{\rm{ }} = {\rm{ }}acos\left( {\omega t} \right)\) trên mặt nước, coi biên độ không đổi, bước sóng \(\lambda = {\rm{ }}3{\rm{ }}cm\) . Gọi O là trung điểm của AB. Một điểm nằm trên đường trung trực AB, dao động cùng pha với các nguồn A và B, cách A hoặc B một đoạn nhỏ nhất là:
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 19 cm, dao động theo phương thẳng đứng với phương trình là \({u_A} = {\rm{ }}{u_B} = {\rm{ }}acos20\pi t\) (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 40 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A. Khoảng cách AM là:
Dùng một âm thoa có tần số rung f = 100Hz người ta tạo ra hai điểm S1,S2 trên mặt nước hai nguồn sóng cùng biên độ,cùng pha.S1S2 = 3,2cm.Tốc độ truyền sóng là 40 cm/s. I là trung điểm của S1S2. Định những điểm dao động cùng pha với I.Tính khoảng từ I đến điểm M gần I nhất dao động cùng pha với I và nằm trên trung trực S1S2 là:
Ba điểm A, B, C trên mặt nước là 3 đỉnh của tam giác đều có cạnh bằng 8cm, trong đó A và B là 2 nguồn phát sóng giống nhau, có bước sóng 0,8cm. Điểm M trên đường trung trực của AB, dao động cùng pha với điểm C và gần C nhất thì phải cách C một khoảng bao nhiêu?
Trên mặt nước có 2 nguồn sóng giống hệt nhau A và B cách nhau một khoảng \(AB = 24cm\). Bước sóng \(\lambda = {\rm{ }}2,5{\rm{ }}cm\). Hai điểm M và N trên mặt nước cùng cách đều trung điểm của đoạn AB một đoạn \(16 cm\) và cùng cách đều 2 nguồn sóng và A và B. Số điểm trên đoạn MN dao động cùng pha với 2 nguồn là:
Có hai nguồn sóng cơ kết hợp A và B trên mặt nước cách nhau một đoạn \(AB = 9\lambda \) phát ra dao động với phương trình \(u{\rm{ }} = {\rm{ }}acos\omega t\) . Xác định trên đoạn AB, số điểm có biên độ cực đại cùng pha với nhau và cùng pha với nguồn, không kể hai nguồn là bao nhiêu?
Trên mặt nước có hai nguồn kết hợp AB cùng pha cách nhau một đoạn 12cm đang dao động vuông góc với mặt nước tạo ra sóng với bước sóng 1,6cm. Gọi C là một điểm trên mặt nước cách đều hai nguồn và cách trung điểm O của đoạn AB một khoản 8cm. Hỏi trên đoạn CO, số điểm dao động cùng pha với nguồn là:
Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12(cm) đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng \(\lambda = {\rm{ }}1,6cm\) . C và D là hai điểm khác nhau trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8(cm). Số điểm dao động cùng pha với nguồn ở trên đoạn CD là
Ba điểm A, B, C trên mặt nước là ba đỉnh của tam giac đều có cạnh 16 cm trong đó A và B là hai nguồn phát sóng có phương trình \({u_1} = {u_2} = 2\cos (20\pi t)(cm)\),sóng truyền trên mặt nước không suy giảm và có vận tốc 20 (cm/s).M trung điểm của AB .Số điểm dao động cùng pha với điểm C trên đoạn MC là:
Hai nguồn phát sóng kết hợp A và B trên mặt chất lỏng dao động theo phương trình:
\({u_A} = {\rm{ }}acos(100\pi t);{\rm{ }}{u_B} = {\rm{ }}bcos(100\pi t)\) . Tốc độ truyền sóng trên mặt chất lỏng 1m/s. I là trung điểm của AB. M là điểm nằm trên đoạn AI, N là điểm nằm trên đoạn IB. Biết \(IM = 5 cm\) và \(IN = 6,5 cm\). Số điểm nằm trên đoạn MN có biên độ cực đại và cùng pha với I là:
Hai mũi nhọn A, B cách nhau \(8 cm\) gắn vào đầu một cần rung có tần số \(f = 100 Hz\), đặt chạm nhẹ vào mặt một chất lỏng. Tốc độ truyền sóng trên mặt chất lỏng \(v = 0,8 m/s\). Hai nguồn A, B dao động theo phương thẳng đứng với cùng phương trình \({u_A} = {\rm{ }}{u_B} = {\rm{ }}acos(\omega t){\rm{ }}cm.\) Một điểm M trên mặt chất lỏng cách đều A, B một khoảng \(d = 8 cm\). Tìm trên đường trung trực của AB hai điểm M1,M2 gần M nhất và dao động cùng pha với M.
Trong thí nghiệm giao thoa sóng mặt nước, 2 nguồn sóng S1 và S2 cách nhau 11cm và dao động điều hòa theo phương vuông góc với mặt nước có cùng phương trình \({u_1} = {u_2} = 5c{\rm{os}}\left( {50\pi t} \right)mm\) . Tốc độ truyền sóng v = 0,5 m/s và biên độ sóng không đổi khi truyền đi. Chọn hệ trục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với S1, Ox trùng S1S2. Trong không gian, phía trên mặt nước có 1 chất điểm chuyển động mà hình chiếu (P) của nó với mặt nước chuyển động với phương trình y = 12 - x và có tốc độ \({v_1} = 5\sqrt 2 cm/s\). Trong thời gian t = 2 (s) kể từ lúc (P) có tọa độ x = 0 thì (P) cắt bao nhiêu vân cực tiểu trong vùng giao thoa của sóng?
Trên mặt nước có hai nguồn kết hợp dao động theo phương vuông góc mặt nước tại hai điểm S1 và S2 với các phương trình lần lượt là: \({u_1} = a.\cos \left( {10\pi t} \right)cm\)và \({u_2} = a.\cos \left( {10\pi t + \dfrac{\pi }{2}} \right)cm\). Biết tốc độ truyền sóng trên mặt nước là 1m/s. Hai điểm M và N thuộc vùng hai sóng giao thoa, biết \(M{S_1}-M{S_2} = 5cm\)và \(N{S_1}-N{S_2} = 35cm\). Chọn phát biểu đúng?
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng . Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước dao động.Biết OM= 8λ; ON =12λ và OM vuông góc ON.Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là
Ở mặt chất lỏng, tại hai điểm A và B cách nhau 28 cm có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng λ = 5cm. Điểm C trên mặt chất lỏng sao cho tam giác ABC vuông cân tại A. Số điểm dao động ngược pha với hai nguồn trên đoạn AC là
