SỐ LƯỢNG CÓ HẠN VÀ TẶNG MIỄN PHÍ THÊM BỘ SÁCH ĐỀ TỔNG HỢP
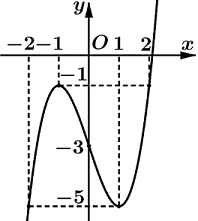
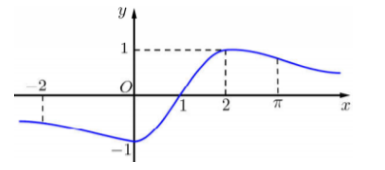
Cho hàm số y=f(x) xác định và liên tục trên R, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn [−2;2].
-
A.
m=−5,M=−1.
-
B.
m=−1,M=0.
-
C.
m=−2,M=2.
-
D.
m=−5,M=0.
Quan sát đồ thị hàm số trên [−2;2] tìm GTLN (điểm cao nhất) và GTNN (điểm thấp nhất) của hàm số.
Dựa vào đồ thị hàm số ta có: {m=min[−2;2]f(x)=−5M=max[−2;2]f(x)=−1.
Đáp án : A

Các bài tập cùng chuyên đề
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=sinx trên đoạn [−π2;−π3] lần lượt là
Cho biết GTLN của hàm số f(x) trên [1;3] là M=−2. Chọn khẳng định đúng:
Cho hàm số f(x) xác định trên [0;2] và có GTNN trên đoạn đó bằng 5. Chọn kết luận đúng:
Giá trị nhỏ nhất của hàm số y=2x+cosx trên đoạn [0;1] là :
Cho hàm số f(x) xác định và liên tục trên R, có limx→+∞f(x)=+∞;limx→−∞f(x)=−∞ , khi đó:
Gọi m là giá trị nhỏ nhất của hàm số y=x−1+4x−1 trên khoảng (1;+∞). Tìm m?
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, chọn kết luận đúng:
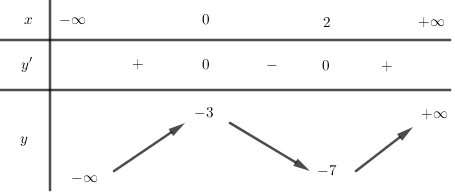
Cho hàm số y=f(x) có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
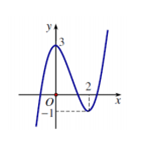
Cho hàm số y=f(x) có bảng biến thiên như sau:
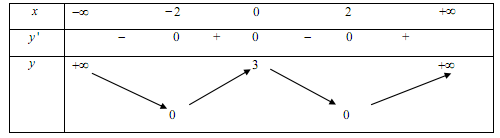
Khẳng định nào sau đây là khẳng định đúng?
Tìm giá trị lớn nhất của hàm số y=x3−5x2+3x−1 trên đoạn [2;4]
Tìm GTLN và GTNN của hàm số y=x5−5x4+5x3+1 trên đoạn [−1;2]
Giá trị lớn nhất của hàm số f(x)=6−8xx2+1 trên tập xác định của nó là:
Gọi giá trị lớn nhất và nhỏ nhất của hàm số y=x4+2x2−1 trên đoạn [−1;2] lần lượt là M và m. Khi đó giá trị của M.m là:
Cho hàm số y=x+1x. Giá trị nhỏ nhất của hàm số trên khoảng (0;+∞) là:
Cho hàm số y=2mx+1m−x. Giá trị lớn nhất của hàm số trên [2;3] bằng −13 khi m bằng:
Cho hàm số y=x3−3mx2+6, giá trị nhỏ nhất của hàm số trên [0;3] bằng 2 khi:
Cho các số thực x,y thỏa mãn (x−4)2+(y−4)2+2xy⩽32. Giá trị nhỏ nhất m của biểu thức A=x3+y3+3(xy−1)(x+y−2) là:
Có bao nhiêu số nguyên m∈[−5;5] để min[1;3]|x3−3x2+m|≥2.
Cho hai số thực x,y thỏa mãn x2+y2−4x+6y+4+√y2+6y+10=√6+4x−x2. Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T=|√x2+y2−a|. Có bao nhiêu giá trị nguyên thuộc đoạn [−10;10] của tham số a để M≥2m?
Cho f(x) mà đồ thị hàm số y=f′(x) như hình vẽ bên
Bất phương trình f(x)>sinπx2+m nghiệm đúng với mọi x∈[−1;3] khi và chỉ khi:

















