Đề bài

Trong hình dưới đây cho biết \(\widehat {{M_4}} = \widehat {{N_2}} = {100^0}\). Tính các góc tại đỉnh \(M,N.\)

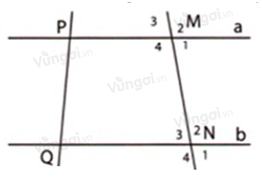
• A. \(\widehat {{M_1}} = \widehat {{M_3}} = \widehat {{N_1}} = \widehat {{N_3}} = {80^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0}\)
• B. \(\widehat {{M_1}} = \widehat {{N_1}} = {80^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0};\widehat {{M_3}} = \widehat {{N_3}} = {60^0}\)
• C. \(\widehat {{M_1}} = \widehat {{M_3}} = {80^0};\widehat {{N_1}} = \widehat {{N_3}} = {70^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0}\)
• D. \(\widehat {{M_1}} = \widehat {{M_3}} = \widehat {{N_4}} = \widehat {{N_3}} = {80^0};\widehat {{M_2}} = \widehat {{N_1}} = {100^0}\)

Phương pháp giải

Sử dụng:

+ Hai góc đối đỉnh thì bằng nhau

+ Tổng hai góc kề bù bằng \({180^0}\)

Lời giải của GV Loigiaihay.com

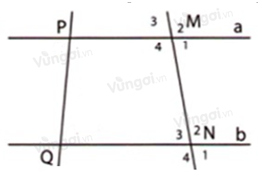
+ Tại \(M\):

Vì \(\widehat {{M_2}};\widehat {{M_4}}\) là hai góc đối đỉnh nên \(\widehat {{M_2}} = \widehat {{M_4}} = {100^0}\) (tính chất hai góc đối đỉnh)

Ta có: \(\widehat {{M_4}};\widehat {{M_1}}\) là hai góc kề bù nên \(\widehat {{M_4}} + \widehat {{M_1}} = {180^0}\) \( \Rightarrow \widehat {{M_1}} = {180^0} - \widehat {{M_4}} = {180^0} - {100^0} = {80^0}\)

Vì \(\widehat {{M_3}};\widehat {{M_1}}\) là hai góc đối đỉnh nên \(\widehat {{M_3}} = \widehat {{M_1}} = {80^0}\) (tính chất hai góc đối đỉnh)

+ Tại \(N\):

Vì \(\widehat {{N_2}};\widehat {{N_4}}\) là hai góc đối đỉnh nên \(\widehat {{N_4}} = \widehat {{N_2}} = {100^0}\) (tính chất hai góc đối đỉnh)

Ta có: \(\widehat {{N_2}};\widehat {{N_3}}\) là hai góc kề bù nên \(\widehat {{N_2}} + \widehat {{N_3}} = {180^0}\) \( \Rightarrow \widehat {{N_3}} = {180^0} - \widehat {{N_2}} = {180^0} - {100^0} = {80^0}\)

Vì \(\widehat {{N_3}};\widehat {{N_1}}\) là hai góc đối đỉnh nên \(\widehat {{N_3}} = \widehat {{N_1}} = {80^0}\) (tính chất hai góc đối đỉnh)

Vậy \(\widehat {{M_1}} = \widehat {{M_3}} = \widehat {{N_1}} = \widehat {{N_3}} = {80^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0}\).

Đáp án : A