Cặp số \(\left( { - 2; - 3} \right)\) là nghiệm của hệ phương trình nào sau đây?
-
A.
\(\left\{ \begin{array}{l}x - y = 3\\2x + y = 4\end{array} \right.\)
-
B.
$\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 8\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 7\end{array} \right.$
-
D.
$\left\{ \begin{array}{l}4x - 2y = 0\\x - 3y = 5\end{array} \right.$
Cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) khi và chỉ khi nó thỏa mãn cả hai phương trình của hệ.
+) Thay $x = - 2;y = - 3$ vào hệ \(\left\{ \begin{array}{l}x - y = 3\\2x + y = 4\end{array} \right.\) ta được $\left\{ \begin{array}{l} - 2 - \left( { - 3} \right) = 1 \ne 3\\2.\left( { - 2} \right) - 3 = - 7 \ne 4\end{array} \right.$ nên loại A.
+) Thay $x = - 2;y = - 3$ vào hệ $\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 8\end{array} \right.$ ta được $\left\{ \begin{array}{l}2.\left( { - 2} \right) - \left( { - 3} \right) = - 1\\ - 2 - 3.\left( { - 3} \right) = 7 \ne 8\end{array} \right.$ nên loại B.
+) Thay $x = - 2;y = - 3$ vào hệ $\left\{ \begin{array}{l}4x - 2y = 0\\x - 3y = 5\end{array} \right.$ ta được $\left\{ \begin{array}{l}4.\left( { - 2} \right) - 2.\left( { - 3} \right) = - 2 \ne 0\\ - 2 - 3.\left( { - 3} \right) = 7 \ne 5\end{array} \right.$ nên loại D.
+) Thay $x = - 2;y = - 3$ vào hệ $\left\{ \begin{array}{l}2x - y = - 1\\x - 3y = 7\end{array} \right.$ ta được $\left\{ \begin{array}{l}2.\left( { - 2} \right) - \left( { - 3} \right) = - 1\\ - 2 - 3.\left( { - 3} \right) = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 = - 1\\7 = 7\end{array} \right.$ nên chọn C.
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9\end{array} \right.\) nhận cặp số nào sau đây là nghiệm
-
A.
$\left( { - 21;15} \right)$
-
B.
$\left( {21; - 15} \right)$
-
C.
$\left( {1;1} \right)$
-
D.
$\left( {1; - 1} \right)$
Bài 2 :
Cho hệ phương trình \(\left\{ \begin{array}{l} - mx + y = - 2m\\x + {m^2}y = 9\end{array} \right..\) Tìm các giá trị của tham số \(m\) để hệ phương trình nhận cặp \(\left( {1;2} \right)\) làm nghiệm.
-
A.
$m = 0$
-
B.
$m = -1$
-
C.
$m = -2$
-
D.
$m = 3$
Bài 3 :
Bằng cách tìm giao điểm của hai đường thẳng $d: - 2x + y = 3$ và $d':x + y = 5$ ta tìm được nghiệm của hệ phương trình $\left\{ \begin{array}{l} - 2x + y = 3\\x + y = 5\end{array} \right.$ là $\left( {{x_0};{y_0}} \right)$. Tính ${y_0} - {x_0}$.
-
A.
$\dfrac{{11}}{3}$
-
B.
$\dfrac{{13}}{3}$
-
C.
$5$
-
D.
$\dfrac{{17}}{3}$
Bài 4 :
Cho hệ phương trình: \(\left\{ \begin{array}{l}mx - 2y = 3m\\2x - my = - 4 - 4m\end{array}. \right.\) Tìm các giá trị của tham số \(m\) để cặp số \(\left( { - 1;2} \right)\) là nghiệm của hệ phương trình đã cho.
-
A.
$m = - 1$
-
B.
$m = 1$
-
C.
$m = - 3$
-
D.
$m = 3$
Bài 5 :
Với giá trị nào của m thì hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{4}{5}x + \dfrac{1}{2}y = m + 1\\x - y = 2\end{array} \right.\) có nghiệm x = 3:
-
A.
\(m = \dfrac{1}{2}\)
-
B.
\(m = \dfrac{{19}}{{10}}\)
-
C.
\(m = \dfrac{3}{{10}}\)
-
D.
Không có giá trị \(m\)
Bài 6 :
Hệ phương trình \(\left\{ \begin{array}{l}5x + y = 7\\ - x - 3y = 21\end{array} \right.\) nhận cặp số nào sau đây là nghiệm
-
A.
$\left( {1;2} \right)$
-
B.
$\left( {8; - 3} \right)$
-
C.
$\left( {3; - 8} \right)$
-
D.
$\left( {3;8} \right)$
Bài 7 :
Cho hệ phương trình \(\left\{ \begin{array}{l}\left( {m + 2} \right)x + y = 2m - 8\\{m^2}x + 2y = - 3\end{array} \right..\) Tìm các giá trị của tham số \(m\) để hệ phương trình nhận cặp số \(\left( { - 1;3} \right)\) làm nghiệm.
-
A.
$m = 0$
-
B.
$m = - 2$
-
C.
$m = - 3$
-
D.
$m = 3$
Bài 8 :
Cặp số \(\left( {3; - 5} \right)\) là nghiệm của hệ phương trình nào sau đây?
-
A.
\(\left\{ \begin{array}{l}x - 3y = 1\\x + y = 2\end{array} \right.\)
-
B.
$\left\{ \begin{array}{l}3x + y = 4\\2x - y = 11\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}y = - 1\\x - 3y = 5\end{array} \right.$
-
D.
$\left\{ \begin{array}{l}4x - y = 0\\x - 3y = 0\end{array} \right.$
Bài 9 :
Bằng cách tìm giao điểm của hai đường thẳng $d:4x + 2y = - 5$ và $d':2x - y = - 1$ ta tìm được nghiệm của hệ phương trình $\left\{ \begin{array}{l}4x + 2y = - 5\\2x - y = - 1\end{array} \right.$ là $\left( {{x_0};{y_0}} \right)$. Tính ${x_0}.{y_0}$.
-
A.
$\dfrac{{21}}{{32}}$
-
B.
$ - \dfrac{{21}}{{32}}$
-
C.
$\dfrac{{21}}{8}$
-
D.
$ - \dfrac{{10}}{{12}}$
Bài 10 :
Với giá trị nào của \(a\) thì hệ phương trình \(\left\{ \begin{array}{l}ax + ay = {a^2}\\x + ay = 2\end{array} \right.\) nhận \(\left( { - \dfrac{2}{3}; - \dfrac{4}{3}} \right)\) là nghiệm:
-
A.
\(a = 1\)
-
B.
\(a = - 1\)
-
C.
\(a = - 2\)
-
D.
\(a = 2\)
Bài 11 :
Cho các cặp số sau (0;-1),\((\sqrt{3};2-\sqrt{3})\),\((1;\sqrt{3}-3)\),\((\sqrt{3}+1;1)\). Cặp số nào không là nghiệm của phương trình \((\sqrt{3}-1)x-y=1\)?
-
A.
(0;-1)
-
B.
\((\sqrt{3};2-\sqrt{3})\)
-
C.
\((1;\sqrt{3}-3)\)
-
D.
\((\sqrt{3}+1;1)\)
Bài 12 :
Tìm giá trị của a và b để đường thẳng (d1): \((3a-1)x+2by=56\) và đường thẳng (d2): \(0,5ax-(3b+2)y=3\) cắt nhau tại điểm M(2;-5).
-
A.
\(a=2,\,b=-3\)
-
B.
\(a=8,\,b=-1\)
-
C.
\(a=5,\,b=-1\)
-
D.
\(a=3,\,b=4\)
Bài 13 :
Trong hai cặp số \(\left( {0; - 2} \right)\) và \(\left( {2; - 1} \right),\) cặp số nào là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}x - 2y = 4\\4x + 3y = 5\end{array} \right.?\)
Bài 14 :
Xét bài toán cổ trong tình huống mở đầu. Gọi x là số cam, y là số quýt cần tính \(\left( {x;y \in {\mathbb{N}^*}} \right),\) ta có hệ phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x + y = 17\\10x + 3y = 100\end{array} \right.\)
Trong hai cặp số \(\left( {10;7} \right)\) và \(\left( {7;10} \right),\) cặp số nào là nghiệm của hệ phương trỉnh trên? Từ đó cho biết phương án về số cam và số quýt thỏa mãn yêu cầu của bài toán cổ.
Bài 15 :
Cho hệ phương trình\(\left\{ {\begin{array}{*{20}{c}}{x + 5y = 10}\\{2x - y = - 13.}\end{array}} \right.\)
Trong hai cặp số (0;2) và (-5;3), cặp số nào là nghiệm của hệ phương trình đã cho?
Bài 16 :
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{4x - y = 2}\\{x + 3y = 7.}\end{array}} \right.\)
Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
a) (2;2)
b) (1;2)
c) (-1;-2).
Bài 17 :
Cặp số (-2;-3) là nghiệm của hệ phương trình nào sau đây?
A. \(\left\{ {\begin{array}{*{20}{c}}{x - 2y = 3}\\{2x + y = 4}\end{array}} \right.\)
B. \(\left\{ {\begin{array}{*{20}{c}}{2x - y = - 1}\\{x - 3y = 8}\end{array}} \right.\)
C. \(\left\{ {\begin{array}{*{20}{c}}{2x - y = - 1}\\{x - 3y = 7}\end{array}} \right.\)
D. \(\left\{ {\begin{array}{*{20}{c}}{4x - 2y = 0}\\{x - 3y = 5}\end{array}} \right.\)
Bài 18 :
Cho hệ phương trình: \(\left\{ \begin{array}{l}2x - 5y = - 2\\x + y = 6\end{array} \right.\).
Kiểm tra xem cặp số nào sau đây là nghiệm của phương trình đã cho:
a. \(\left( {3;3} \right)\);
b. \(\left( {4;2} \right)\).
Bài 19 :
Cho hệ phương trình: \(\left\{ \begin{array}{l}x + 2y = 1\\3x - 2y = 3\,\,.\end{array} \right.\)
Trong các cặp số sau, cặp số nào là nghiệm của hệ phương trình đã cho?
a. \(\left( {3; - 1} \right)\);
b. \(\left( {1;0} \right)\).
Bài 20 :
Xét hệ hai phương trình bậc nhất hai ẩn
\(\left\{ \begin{array}{l}x + y = 45\\3x + y = 105.\end{array} \right.\)
Trong hai cặp số \(\left( {25;20} \right)\) và \(\left( {30;15} \right)\), cặp số nào là một nghiệm của phương trình \(x + y = 45\), đồng thời là một nghiệm của phương trình \(3x + y = 105\)?
Bài 21 :
Giải thích vì sao hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x - 2y = 3\end{array} \right.\) vô nghiệm.
Bài 22 :
Cho hai phương trình \(x + y = 2\) (1) và \(x - y = 0\) (2). Cặp số nào sau đây là nghiệm của hệ hai phương trình gồm phương trình (1) và (2)?
-
A.
(-1;-1).
-
B.
(-1;3).
-
C.
(1;1).
-
D.
(2;2).
Bài 23 :
Trong các cặp số \(\left( {1;-1} \right),\left( {1;-2} \right),\left( {-3;-7} \right),\left( { 3;-7} \right)\), cặp số nào là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}3x + y = 2\\5x + 2y = 1\end{array} \right.\)?
-
A.
\(\left( {1; - 1} \right)\).
-
B.
\(\left( {1; - 2} \right)\).
-
C.
\(\left( {-3;-7} \right)\).
-
D.
\(\left( { 3;-7} \right)\).
Bài 24 :
Với \(m = 1\) thì hệ phương trình \(\left\{ \begin{array}{l}3mx + y = 0\\x - 5my = - 4\end{array} \right.\) nhận cặp số nào là nghiệm?
-
A.
\(\left( { - \frac{1}{4};\frac{3}{4}} \right)\).
-
B.
\(\left( {\frac{1}{4}; - \frac{3}{4}} \right)\).
-
C.
\(\left( {\frac{3}{4}; - \frac{1}{4}} \right)\).
-
D.
\(\left( { - \frac{3}{4};\frac{1}{4}} \right)\).
Bài 25 :
Cho hệ phương trình \(\left\{ \begin{array}{l}2x - y = - 20\\\left( {4 - 2m} \right)x + y = 10\end{array} \right.\). Tìm m để hệ phương trình đã cho vô nghiệm.
-
A.
\(m = 3\).
-
B.
\(m = 1\).
-
C.
\(m = - 2\).
-
D.
\(m = - 1\).
Bài 26 :
Cho hai phương trình \( - 3x + y = - 7\;\left( 1 \right)\) và \(x - 2y = 4\;\left( 2 \right)\). Cặp số nào sau đây là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?
A. \(\left( {0; - 7} \right)\).
B. \(\left( {6;1} \right)\).
C. \(\left( {2; - 1} \right)\).
D. \(\left( { - 1; - 10} \right)\).
Bài 27 :
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{3x + 2y = 7}\\{ - x - 4y = - 9}\end{array}} \right.\)
Trong các cặp số (3;2), (1;2), (5;1), cặp số nào là nghiệm của hệ phương trình đã cho?
Bài 28 :
Đường thẳng \(y = ax + b\) đi qua hai điểm (2; -1) và (-4; -3). Khi đó
A. \(a = 1;b = - 3\).
B. \(a = \frac{1}{2};b = - 2\).
C. \(a = \frac{1}{3};b = - \frac{5}{3}\).
D. \(a = 0;b = - 3\).
Bài 29 :
Với giá trị nào của m thì hệ phương trình \(\left\{ \begin{array}{l}3x - {m^2}y = 5\\mx + 5y = 2\end{array} \right.\) nhận (3; 1) là nghiệm?
A. Không có giá trị nào của m thỏa mãn.
B. \(m = 2\).
C. \(m = - 2\).
D. \(m = - 1\).
Bài 30 :
Hình bên dưới minh họa tập nghiệm của hệ phương trình nào sau đây?
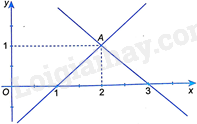
A. \(\left\{ \begin{array}{l}x - y = 1\\x - y = 3\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - y = 1\\x + y = 3\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x + y = 1\\x - y = 3\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x + y = 1\\x + y = 3\end{array} \right.\).


















Danh sách bình luận