Đề bài

Cho \(\Delta ABC\) có \(M\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?

• A. \(AM\) bằng nửa chu vi của tam giác \(ABC\).
• B. \(AM\) nhỏ hơn nửa chu vi của tam giác \(ABC\).
• C. \(AM\) lớn hơn chu vi của tam giác \(ABC\).
• D. \(AM\) lớn hơn nửa chu vi của tam giác \(ABC\).

Phương pháp giải

- Nối đoạn thẳng AM.

- Áp dụng bất đẳng thức tam giác chứng minh: \(AM < AC + CM\), \(AM < AB + MB\). Từ đó lập luận suy ra điều phải chứng minh.

Lời giải của GV Loigiaihay.com

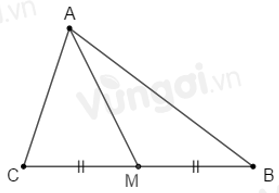
Nối đoạn thẳng AM.

Xét \(\Delta AMC\) có: \(AM < AC + CM\) (bất đẳng thức tam giác)   (1)

Xét \(\Delta AMB\) có: \(AM < AB + MB\) (bất đẳng thức tam giác)    (2)

Vì \(M\) là trung điểm của \(BC\) (gt) nên \(M\) nằm giữa \(B\) và \(C\) ta có: \(CM + MB = BC.\)

Cộng bất đẳng thức (1) và (2) theo vế với vế ta được:

\(\begin{array}{l}AM + AM < AC + CM + AB + MB\\ \Rightarrow 2AM < AB + \left( {CM + MB} \right) + AC\\ \Rightarrow 2AM < AB + BC + AC\\ \Rightarrow AM < \dfrac{{AB + BC + AC}}{2}\end{array}\)

Do đó \(AM\) nhỏ hơn nửa chu vi của tam giác \(ABC\).

Đáp án : B