Đề bài

Cho tam giác $ABC$ vuông tại $A$ có $\widehat B = {30^0}.$ Khi đó:

• A. $AC = \dfrac{{BC}}{2}$
• B. $AB = \dfrac{{BC}}{2}$
• C. $\Delta ABC$ là tam giác vuông cân
• D. $AC = \dfrac{{BC}}{3}$

Phương pháp giải

Lấy điểm $M$ trên cạnh $BC$ sao cho $\widehat {BAM} = {30^o}.$ Chứng minh $\Delta AMB$ cân và $\Delta AMC$ đều suy ra $MA = MB = MC = AC$, từ đó suy ra điều phải chứng minh.

Lời giải của GV Loigiaihay.com

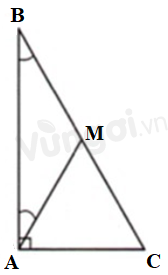
Lấy điểm $M$ trên cạnh $BC$ sao cho $\widehat {BAM} = {30^o}.$

$\Delta AMB$ có $\widehat {BAM} = \widehat B = {30^o}$ nên là tam giác cân, suy ra $MA = MB$            (1)

$\Delta ABC$ vuông tại $A$ nên $\widehat B + \widehat C = {90^o}$ $\Rightarrow \widehat C = {90^o} - \widehat B = {90^o} - {30^o} = {60^o}.$

Ta có: $\widehat {BAC} = \widehat {BAM} + \widehat {MAC}$

$\Rightarrow \widehat {MAC} = \widehat {BAC} - \widehat {BAM} = {90^o} - {30^o} = {60^o}.$

$\Delta AMC$ có: $\widehat {MAC} = \widehat C = {60^o}$ nên là tam giác đều, suy ra $AC = AM = MC$   (2)

Từ (1) và (2) ta có: $AC = MB = MC$ hay $AC = \dfrac{{BC}}{2}.$

Đáp án : A