Cho \(M\) thuộc đoạn thẳng \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB,\) vẽ các tam giác đều \(AMC,BMD.\) Gọi \(E;F\) theo thứ tự là trung điểm của \(AD;BC.\) Tam giác \(MEF\) là tam giác gì? Chọn câu trả lời đúng nhất.
-
A.
Tam giác nhọn
-
B.
Tam giác cân
-
C.
Tam giác đều
-
D.
Cả A, B, C đều đúng
- Sử dụng:
- Tính chất: Tam giác đều có ba cạnh bằng nhau, ba góc bằng nhau và cùng bằng \({60^o}.\)
- Trường hợp bằng nhau thứ hai của tam giác: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Dấu hiệu nhận biết tam giác đều: Tam giác cân có một góc bằng \({60^o}.\)
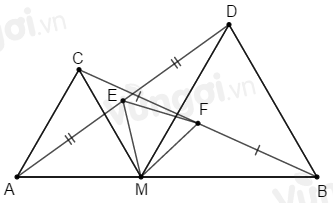
\(\Delta AMC\) đều nên \(\widehat {AMC} = {60^o};\,AM = CM.\)
\(\Delta BMD\) đều nên \(\widehat {BMD} = {60^o};\,MD = MB.\)
\(\widehat {AMD} = \widehat {AMC} + \widehat {CMD} = {60^o} + \widehat {CMD}\) (1)
\(\widehat {CMB} = \widehat {BMD} + \widehat {CMD} = {60^o} + \widehat {CMD}\) (2)
Từ (1) và (2) suy ra: \(\widehat {AMD} = \widehat {CMB}\)
Xét \(\Delta AMD\) và \(\Delta CMB\) có:
\(AM = CM\,\,(cmt)\)
\(\widehat {AMD} = \widehat {CMB}\,\,(cmt)\)
\(MD = MB\,\,(cmt)\)
\( \Rightarrow \Delta AMD = \Delta CMB\,(c.g.c)\)
\( \Rightarrow AD = CB\) (hai cạnh tương ứng).
\( \Rightarrow \widehat {DAM} = \widehat {BCM}\) (hai góc tương ứng).
Xét \(\Delta AEM\) và \(\Delta CFM\) có:
\(AM = CM\,(cmt)\)
\(\widehat {DAM} = \widehat {BCM}\,(cmt)\)
\(AE = CF\,\,\left( {\dfrac{{AD}}{2} = \dfrac{{CB}}{2}} \right)\)
\( \Rightarrow \Delta AEM = \Delta CFM\,(c.g.c)\)
\( \Rightarrow EM = FM\) (hai cạnh tương ứng).
\( \Rightarrow \widehat {AME} = \widehat {CMF}\) (hai góc tương ứng)
\( \Rightarrow \widehat {AMC} + \widehat {CME} = \widehat {CME} + \widehat {EMF}\)
\( \Rightarrow \widehat {AMC} = \widehat {EMF}\)
\( \Rightarrow \widehat {EMF} = {60^o}\)
Xét \(\Delta MEF\) có: \(EM = FM\,(cmt);\,\widehat {EMF} = {60^o}\,(cmt)\) nên \(\Delta MEF\) là tam giác đều.
Tam giác đều vừa là tam giác cân vừa là tam giác nhọn (vì có ba góc nhọn) nên cả A, B, C đều đúng.
Đáp án : D
Các bài tập cùng chuyên đề
Chọn câu sai.
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
Số tam giác cân trong hình vẽ dưới đây là:
Tính số đo \(x\) trên hình vẽ sau:
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = {30^0}.\) Khi đó:
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:
Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)
Cho tam giác \(ABC\) cân tại \(B,\,\widehat {BAC} = {80^0}.\) Lấy \(I\) là điểm nằm trong tam giác sao cho \(\widehat {IAC} = {10^0};\widehat {ICA} = {30^0}.\) Tính góc \(ABI.\)
