Đề bài

Có bao nhiêu cặp số \(a;b \in Z\) thỏa mãn \(\dfrac{a}{5} + \dfrac{1}{{10}} = \dfrac{{ - 1}}{b}\)?

• A. \(0\)
• B. Không tồn tại \((a;b)\)
• C. \(4\)
• D. \(10\)

Phương pháp giải

Ta quy đồng phân số để tìm a, b.

Lời giải của GV Loigiaihay.com

\(\begin{array}{l}\dfrac{a}{5} + \dfrac{1}{{10}} = \dfrac{{ - 1}}{b}\\\dfrac{{2{\rm{a}}}}{{10}} + \dfrac{1}{{10}} = \dfrac{{ - 1}}{b}\\\dfrac{{2{\rm{a}} + 1}}{{10}} = \dfrac{{ - 1}}{b}\\\left( {2{\rm{a}} + 1} \right).b =  - 10\end{array}\)

\(2{\rm{a}} + 1\) là số lẻ; \(2{\rm{a}} + 1\) là ước của \( - 10\)

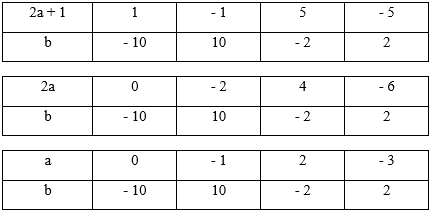
Vậy có \(4\) cặp số \((a;b)\) thỏa mãn bài toán.

Đáp án : C