Cho tam giác ABC có ˆA=900,M là trung điểm AC. Trên tia đối của tia MB lấy K sao cho MK=MB. Chọn câu đúng nhất:
-
A.
KC⊥AC
-
B.
AK//BC
-
C.
AK=CB
-
D.
Cả A, B, C đều đúng
Sử dụng trường hợp bằng nhau thứ hai của tam giác để chứng minh ΔABM=ΔCKM và ΔAMK=ΔCMB, từ đó suy ra các góc tương ứng bằng nhau và lí luận để suy ra điều phải chứng minh.
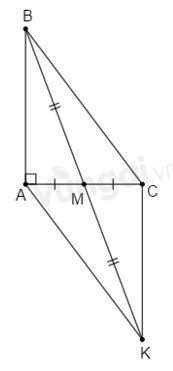
Xét ΔABM và ΔCKM có:
AM=CM (vì M là trung điểm AC)
MB=MK(gt)
^AMB=^CMK (hai góc đối đỉnh)
⇒ΔABM=ΔCKM(c.g.c)
⇒^BAM=^KCM (hai góc tương ứng).
Mà ^BAM=90o (vì ΔABC vuông tại A) suy ra ^KCM=90o.
Do đó KC⊥AC (A đúng).
Xét ΔAMK và ΔCMB có:
AM=CM (vì M là trung điểm AC)
MK=MB(gt)
^AMK=^CMB (hai góc đối đỉnh)
⇒ΔAMK=ΔCMB(c.g.c)
⇒AK=CB (hai cạnh tương ứng) (C đúng).
⇒^MAK=^MCB (hai góc tương ứng).
Mà ^MAK và ^MCB ở vị trí so le trong nên AK//BC (B đúng).
Đáp án : D

Các bài tập cùng chuyên đề
Cho tam giác ABC và tam giác MHK có: AB=MH , ˆA=ˆM. Cần thêm một điều kiện gì để hai tam giác ABC và MHK bằng nhau theo trường hợp cạnh – góc – cạnh:
Cho tam giác BAC và tam giác KEF có BA=EK, ˆA=ˆK, CA=KF. Phát biểu nào trong trong các phát biểu sau đây là đúng:
Cho hai đoạn thẳng BD và EC vuông góc với nhau tại A sao cho AB=AE,AD=AC,AB<AC. Phát biểu nào trong các phát biểu sau đây là sai:
Cho tam giác DEF và tam giác HKG có DE=HK , ˆE=ˆK, EF=KG. Biết ˆD=700. Số đo góc H là:
Cho tam giác ABC có ˆA=900, tia phân giác BD của góc B (D∈AC). Trên cạnh BC lấy điểm E sao cho BE=BA. Hai góc nào sau đây bằng nhau?
Cho đoạn thẳng AB, trên đường trung trực d của đoạn AB lấy điểm M. So sánh AM và BM.
Cho tam giác ABC có M,N lần lượt là trung điểm của AB,AC. Trên tia đối của tia MC lấy D sao cho MD=MC . Trên tia đối của tia NB lấy điểm E sao cho NE=NB.
(I) ΔAMD=ΔBMC
(II) ΔANE=ΔCNB
(III) A,D,E thẳng hàng
(IV) A là trung điểm của đoạn thẳng DE
Số khẳng định đúng trong các khẳng định trên là
Cho hai đoạn thẳng AB và CD cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó. Lấy E;F lần lượt là điểm thuộc đoạn AD và BC sao cho AE=BF. Cho OE=2cm, tính EF.

















