Đề bài

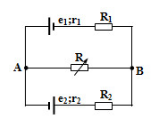
Cho mạch như hình vẽ: E₁ = 24V, E₂ = 6V, r₁ = r₂ = 1$\Omega $; R₁ = 5$\Omega $; R₂ = 2$\Omega $. R là biến trở. Với giá trị nào của biến trở thì công suất trên R đạt cực đại, giá trị cực đại đó là?

• A. 4W
• B. 2W
• C. 3W
• D. 1W

Lời giải của GV Loigiaihay.com

Ta xét nguồn tương đương gồm hai nhánh chứa hai nguồn E₁ và E₂

Giả sử cực dương của nguồn tương đương ở A, chiều dòng điện như hình vẽ:

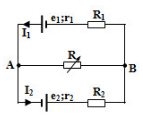
Biến trở R là mạch ngoài:

\(\frac{1}{{{r_b}}} = \frac{1}{{{r_1} + {R_1}}} + \frac{1}{{{r_2} + {R_2}}} \to {r_b} = 2\Omega \)

\({E_b} = \frac{{\frac{{{E_1}}}{{{r_1} + {R_1}}} - \frac{{{E_2}}}{{{r_2} + {R_2}}}}}{{\frac{1}{{{r_b}}}}} = 4V = {U_{AB}}\)

Mạch tương đương:

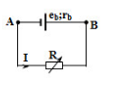
Để công suất trên R cực đại thì : R = r_b = 2$\Omega $

\({P_{{\rm{max}}}} = \frac{{E_b^2}}{{4{{\rm{r}}_b}}} = 2{\rm{W}}\)

Đáp án : B