Một vật bắt đầu trượt không ma sát từ đỉnh mặt phẳng nghiêng dài \(20m\) nghiêng góc \({30^0}\) so với phương ngang. Bỏ qua ma sát trên mặt phẳng nghiêng.
Tính vận tốc của vật tại chân mặt phẳng nghiêng
Tính vận tốc của vật tại chân mặt phẳng nghiêng
\(10\sqrt 2 m/s\)
\(2\sqrt 5 m/s\)
\(2\sqrt {10} m/s\)
\(5\sqrt 2 m/s\)
Đáp án : A
+ Sử dụng biểu thức tính thế năng: \({{\rm{W}}_t} = mgz\)
+ Sử dụng biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
+ Sử dụng biểu thức tính cơ năng và định luật bảo toàn cơ năng: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = h/s\)
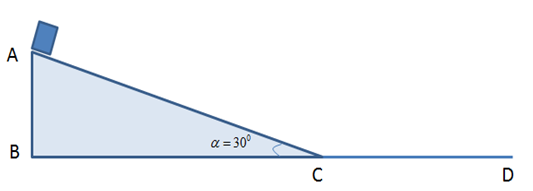
Chọn mốc thế năng tại mặt đất, ta có:
+ Tại A:
- Động năng của vật bằng 0 (do vật bắt đầu trượt => \({v_0} = 0m/s\))
- Thế năng của vật \({{\rm{W}}_{{t_A}}} = mg{h_A} = mgAB\)
Lại có: \(\sin \alpha = \dfrac{{AB}}{{AC}} \Rightarrow AB = AC\sin \alpha \)
Suy ra cơ năng tại A: \({{\rm{W}}_A} = {{\rm{W}}_{{d_A}}} + {{\rm{W}}_{{t_A}}} = mgAC\sin \alpha \)
+ Tại C:
- Thế năng của vật bằng 0 (do \({h_C} = 0\))
- Động năng của vật: \({{\rm{W}}_{{d_C}}} = \dfrac{1}{2}mv_C^2\)
Cơ năng tại C: \({{\rm{W}}_C} = {{\rm{W}}_{{d_C}}} + {{\rm{W}}_{{t_C}}} = \dfrac{1}{2}mv_C^2\)
+ Do bỏ qua ma sát trên mặt phẳng nghiêng => Cơ năng của vật được bảo toàn
\(\begin{array}{l} \Rightarrow {{\rm{W}}_A} = {{\rm{W}}_C}\\ \Leftrightarrow mgAC\sin \alpha = \dfrac{1}{2}mv_C^2\\ \Rightarrow {v_C} = \sqrt {2gAC\sin \alpha } \\ = \sqrt {2.10.20.\sin {{30}^0}} = 10\sqrt 2 m/s\end{array}\)

Vật tiếp tục chuyển động trên mặt phẳng ngang thêm \(100m\) thì dừng hẳn. Hệ số ma sát trên mật phẳng ngang là
Vật tiếp tục chuyển động trên mặt phẳng ngang thêm \(100m\) thì dừng hẳn. Hệ số ma sát trên mật phẳng ngang là
\(0,02\)
\(0,01\)
\(0,1\)
\(1\)
Đáp án : C
+ Sử dụng biểu thức tính thế năng: \({{\rm{W}}_t} = mgz\)
+ Sử dụng biểu thức tính động năng: \({{\rm{W}}_d} = \dfrac{1}{2}m{v^2}\)
+ Sử dụng biểu thức tính công: \(A = Fs\cos \alpha \)
+ Sử dụng biểu thức tính lực ma sát: \({F_{ms}} = \mu N\)
+ Sử dụng định lí biến thiên cơ năng, ta có: \({{\rm{W}}_2} - {{\rm{W}}_1} = A\)
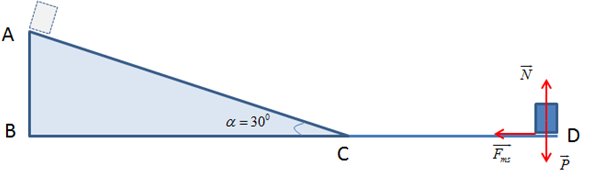
Chọn chiều dương trùng chiều chuyển động của vật
Ta có vật trượt từ A đến điểm C với vận tốc \({v_C} = 10\sqrt 2 m/s\) (đã tính câu trên)
Khi trượt trên mặt phẳng ngang vật chịu tác dụng của lực ma sát => chuyển động chậm dần đến D thì dừng lại
\( \Rightarrow {v_D} = 0m/s\)
Thế năng tại C bằng thế năng tại D và bằng 0
Áp dụng định lí biến thiên cơ năng, ta có: \({{\rm{W}}_D} - {{\rm{W}}_C} = {A_{{F_{ms}}}}\) (1)
+ Ta có:
- Cơ năng tại C: \({{\rm{W}}_C} = {{\rm{W}}_{{d_C}}} + {{\rm{W}}_{{t_C}}} = \dfrac{1}{2}mv_C^2\)
- Cơ năng tại D: \({{\rm{W}}_D} = {{\rm{W}}_{{d_D}}} + {{\rm{W}}_{{t_D}}} = \dfrac{1}{2}mv_D^2 = 0J\)
- Công của lực ma sát: \({A_{{F_{ms}}}} = - {F_{ms}}.CD = - \mu N.CD = - \mu mgCD\)
Thay vào (1), ta được: \(\dfrac{1}{2}mv_D^2 - \dfrac{1}{2}mv_C^2 = - \mu mg.CD\)
\(\begin{array}{l} \Leftrightarrow 0 - \dfrac{1}{2}mv_C^2 = - \mu mgCD\\ \Rightarrow \mu = \dfrac{{v_C^2}}{{2gCD}} = \dfrac{{{{\left( {10\sqrt 2 } \right)}^2}}}{{2.10.100}} = 0,1\end{array}\)

Các bài tập cùng chuyên đề


















Danh sách bình luận