Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \dfrac{{\sqrt {3x - 2} + 6x}}{{\sqrt {4 - 3x} }}.\)
-
A.
\({\rm{D}} = \left[ {\dfrac{2}{3};\dfrac{4}{3}} \right).\)
-
B.
\({\rm{D}} = \left[ {\dfrac{3}{2};\dfrac{4}{3}} \right).\)
-
C.
\({\rm{D}} = \left[ {\dfrac{2}{3};\dfrac{3}{4}} \right).\)
-
D.
\({\rm{D}} = \left( { - \infty ;\dfrac{4}{3}} \right).\)
Hàm số \(y = \sqrt {f\left( x \right)} \) xác định nếu \(f\left( x \right)\) xác định và \(f\left( x \right) \ge 0\).
Hàm số \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định khi \(g\left( x \right) \ne 0\).
Hàm số xác định khi \(\left\{ \begin{array}{l}3x - 2 \ge 0\\4 - 3x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{2}{3}\\x < \dfrac{4}{3}\end{array} \right. \Leftrightarrow \dfrac{2}{3} \le x < \dfrac{4}{3}.\)
Vậy tập xác định của hàm số là \({\rm{D}} = \left[ {\dfrac{2}{3};\dfrac{4}{3}} \right)\).
Đáp án : A

Các bài tập cùng chuyên đề
Bài 1 :
Tập xác định của hàm số \(y = \dfrac{{x - 1}}{{{x^2} - x + 3}}\) là
-
A.
\(\emptyset \).
-
B.
\(\mathbb{R}\).
-
C.
\(\mathbb{R} \backslash \left\{ 1 \right\}\).
-
D.
\(\mathbb{R} \backslash \left\{ 0 \right\}\).
Bài 2 :
Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \dfrac{{3x - 1}}{{2x - 2}}\).
-
A.
\({\rm{D}} = \mathbb{R}.\)
-
B.
\({\rm{D}} = \left( {1; + \infty } \right).\)
-
C.
\({\rm{D}} = \mathbb{R}\backslash \left\{ 1 \right\}.\)
-
D.
\({\rm{D}} = \left[ {1; + \infty } \right).\)
Bài 3 :
Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \dfrac{{2x + 1}}{{{x^3} - 3x + 2}}.\)
-
A.
\({\rm{D}} = \mathbb{R}\backslash \left\{ {1;2} \right\}.\)
-
B.
\({\rm{D}} = \mathbb{R}\backslash \left\{ { - 2;1} \right\}.\)
-
C.
\({\rm{D}} = \mathbb{R}\backslash \left\{ { - 2} \right\}.\)
-
D.
\({\rm{D}} = \mathbb{R}.\)
Bài 4 :
Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {x + 2} - \sqrt {x + 3} .\)
-
A.
\({\rm{D}} = \left[ { - 3; + \infty } \right).\)
-
B.
\({\rm{D}} = \left[ { - 2; + \infty } \right).\)
-
C.
\({\rm{D}} = \mathbb{R}.\)
-
D.
\({\rm{D}} = \left[ {2; + \infty } \right).\)
Bài 5 :
Tìm tập xác định của hàm số \(y = \sqrt {x - 1} + \dfrac{1}{{x + 4}}.\)
-
A.
\(\left[ {1; + \infty } \right)\backslash \left\{ 4 \right\}.\)
-
B.
\(\left( {1; + \infty } \right)\backslash \left\{ 4 \right\}.\)
-
C.
\(\left( { - 4; + \infty } \right).\)
-
D.
\(\left[ {1; + \infty } \right).\)
Bài 6 :
Tìm tập xác định của hàm số \(y = \sqrt {x + 2} - \dfrac{2}{{x - 3}}\).-
A.
\(\mathbb{R}\)\{3}
-
B.
\(\left( {3; + \infty } \right)\)
-
C.
\(\left( { - 2; + \infty } \right)\)
-
D.
\(\left[ { - 2; + \infty } \right)\backslash \left\{ 3 \right\}\)
Bài 7 :
Tập xác định của hàm số \(y = \frac{{x - 2}}{{x + 3}}\) là:
-
A.
R
-
B.
R\{2}
-
C.
R\{-3}
-
D.
R\{2;-3}
Bài 8 :
Tập giá trị của hàm số \(y = \sin x\) là:
-
A.
\(\mathbb{R}\)
-
B.
\([0;1]\)
-
C.
\([0; + \infty )\)
-
D.
\([ - 1;1]\)
Bài 9 :
Tìm tập xác định của mỗi hàm số sau:
a) \(y = - {x^2}\)
b) \(y = \sqrt {2 - 3x} \)
c) \(y = \frac{4}{{x + 1}}\)
d) \(y = \left\{ \begin{array}{l}1{\rm{ khi }}x \in \mathbb{Q}\\0{\rm{ khi }}x \in \mathbb{R}\backslash \mathbb{Q}\end{array} \right.\)
Bài 10 :
Tìm tập xác định của mỗi hàm số sau:
a) \(y = \frac{1}{{{x^2} - x}}\)
b) \(y = \sqrt {{x^2} - 4x + 3} \)
c) \(y = \frac{1}{{\sqrt {x - 1} }}\)
Bài 11 :
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt {2x + 7} \)
b) \(f(x) = \frac{{x + 4}}{{{x^2} - 3x + 2}}\)
Bài 12 :
Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
|
t (giây) |
0,5 |
1 |
1,2 |
1,8 |
2,5 |
|
v (mét/giây) |
1,5 |
3 |
0 |
5,4 |
7,5 |
Vì sao bảng này biểu thị một hàm số? Tìm tập xác định của hàm số này.
Bài 13 :
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt { - 5x + 3} \)
b) \(f(x) = 2 + \frac{1}{{x + 3}}\)
Bài 14 :
Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
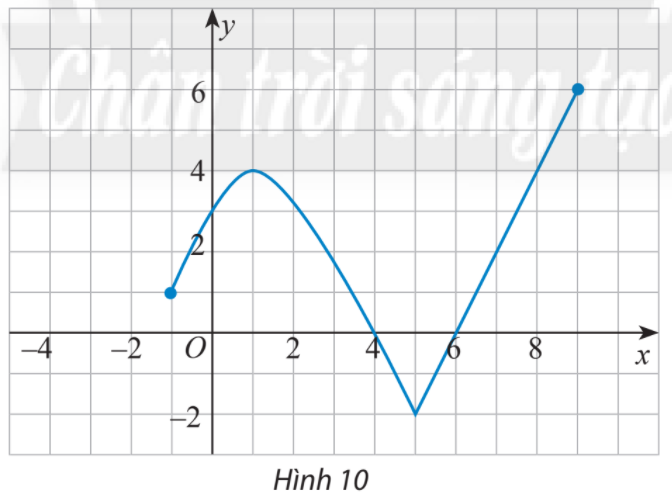
Bài 15 :
Tìm tập xác định của các hàm số sau:
a) \(y = 4{x^2} - 1\)
b) \(y = \dfrac{1}{{{x^2} + 1}}\)
c) \(y = 2 + \dfrac{1}{x}\)
Bài 16 :
Tìm tập xác định của mỗi hàm số sau:
a) \(y = - {x^3} + 4x - 1\)
b) \(y = \sqrt {5 - 6x} \)
c) \(y = \frac{4}{{3x + 1}}\)
d) \(y = \frac{1}{{2x - 1}} - \sqrt {3 - x} \)
e) \(y = \frac{{2x + 3}}{{{x^2} + 3x - 4}}\)
g) \(y = \left\{ \begin{array}{l}x - 1,x > 0\\5x + 1,x < - 1\end{array} \right.\)
Bài 17 :
Cho hàm số \(y = \left\{ \begin{array}{l} - x + 1,x < 0\\0,x = 0\\1,x > 0\end{array} \right.\)
a) Tìm tập xác định của hàm số trên.
b) Tính giá trị của hàm số khi \(x = - 2,x = 0,x = 2021\).
Bài 18 :
Tìm tập xác định của các hàm số sau:
a) \(f\left( x \right) = \frac{{4x - 1}}{{\sqrt {2x - 5} }}\)
b) \(f\left( x \right) = \frac{{2 - x}}{{\left( {x + 3} \right)\left( {x - 7} \right)}}\)
c) \(f\left( x \right) = \left\{ \begin{array}{l}\frac{1}{{x - 3}}{\rm{ }}\quad \;\;x \ge {\rm{0 }}\\1{\rm{ }}\quad {\rm{ }}x < 0\end{array} \right.\)
Bài 19 :
Hàm số \(y = f\left( x \right) = \sqrt {x - 1} + \frac{1}{{{x^2} - 9}}\) có tập xác định là:
A. \(D = \left[ {1; + \infty } \right)\)
B. \(D = \mathbb{R}\backslash \left\{ { - 3;3} \right\}\)
C. \(D = \left[ {1; + \infty } \right)\backslash \left\{ 3 \right\}\)
D. \(D = \left[ {3; + \infty } \right)\)
Bài 20 :
Tập giá trị của hàm số \(y = f\left( x \right) = - 2{x^2} + \sqrt 2 x + 1\) là:
A. \(T = \left( { - \frac{5}{4}; + \infty } \right)\)
B. \(T = \left[ { - \frac{5}{4}; + \infty } \right)\)
C. \(T = \left( { - \infty ;\frac{5}{4}} \right)\)
D. \(T = \left( { - \infty ;\frac{5}{4}} \right]\)
Bài 21 :
a) Hãy cho biết Bảng 6.4 có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của hàm số đó.

b) Trở lại HĐ2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại x = 2018. Tìm tập xác định, tập giá trị của hàm số đó.
c) Cho hàm số \(y = f(x) = - 2{x^2}\). Tính f(1); f(2) và tìm tập xác định, tập giá trị của hàm số này.
Bài 22 :
Tìm tập xác định của các hàm số sau:
a) \(y = 2{x^3} + 3x + 1\)
b) \(y = \frac{{x - 1}}{{{x^2} - 3x + 2}}\)
c) \(y = \sqrt {x + 1} + \sqrt {1 - x} \)
Bài 23 :
Tìm tập xác định và tập giá trị của mỗi hàm số sau:
a) \(y = 2x + 3\)
b) \(y = 2{x^2}\)
Bài 24 :
Tìm tập xác định của hàm số \(y = \frac{1}{{\sqrt {x - 2} }}\) là:
A. \(D = \left[ {2; + \infty } \right).\)
B. \(D = \left( {2; + \infty } \right).\)
C. \(D = \mathbb{R}\backslash \left\{ 2 \right\}.\)
D. \(D = \mathbb{R}.\)
Bài 25 :
Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {2x - 1} + \sqrt {5 - x} \)
b) \(y = \frac{1}{{\sqrt {x - 1} }}.\)
Bài 26 :
Tìm tập xác định của mỗi hàm số sau:
a) \(f(x) = \frac{1}{{2x - 4}}\)
b) \(f(x) = \frac{{{x^2}}}{{{x^2} - 3x + 2}}\)
c) \(f(x) = \sqrt {2x - 3} \)
d) \(f(x) = \frac{3}{ \sqrt {4-x}}\)
Bài 27 :
Cho bảng các giá trị tương ứng của hai đại lượng x và y. Đại lượng y có là hàm số của đại lượng x không? Nếu có, hãy tìm tập xác định và tập giá trị của hàm số đó.
a)
|
x |
-5 |
-3 |
-1 |
0 |
1 |
2 |
5 |
8 |
9 |
|
y |
-6 |
-8 |
-4 |
1 |
3 |
2 |
3 |
12 |
15 |
b)
|
x |
-10 |
-8 |
-4 |
2 |
3 |
6 |
7 |
6 |
13 |
|
y |
-16 |
-14 |
-2 |
4 |
5 |
20 |
18 |
24 |
25 |
Bài 28 :
Tìm tập xác định và tập giá trị của các hàm số bậc hai sau:
a) \(f(x) = - {x^2} + 4x - 3\)
b) \(f(x) = {x^2} - 7x + 12\)
Bài 29 :
Thu nhập bình quân theo đầu người (GDP) của Việt Nam (tính theo USD) trong vòng 10 năm, từ năm 2009 đến năm 2018 được cho bởi bảng sau (dựa theo số liệu của Tổng cục Thống kê):
Bảng này xác định một hàm số chỉ sự phụ thuộc của GDP (kí hiệu là y) vào thời gian x (tính bằng năm). Khẳng định nào dưới đây là sai?
A. Giá trị của hàm số tại x = 2018 là 2 587
B. Tập xác định của hàm số có 10 phần tử
C. Tập giá trị của hàm số có 10 phẩn tử
D. Giá trị của hàm số tại x = 2587 là 2018
Bài 30 :
Tập xác định của hàm số \(y = \sqrt x \) là:
A. \(\mathbb{R}\backslash {\rm{\{ }}0\} \)
B. \(\mathbb{R}\)
C. \(\left[ {0; + \infty } \right)\)
D. \(\left( {0; + \infty } \right)\)



















Danh sách bình luận