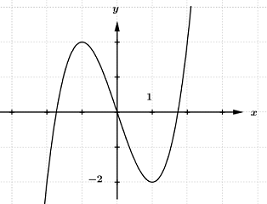
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + 4m + 4} \right)\) có nghiệm?
-
A.
\(4\).
-
B.
\(5\).
-
C.
Vô số
-
D.
\(3\).
+ Đặt \(\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}} = t\), biến đổi đưa về dạng \(a\sin x + b\cos x = c\), phương trình này có nghiệm khi \({a^2} + {b^2} \ge {c^2}\) từ đó ta tìm ra được điều kiện của \(t.\)
+ Dựa vào đồ thị hàm số để xác định điều kiện nghiệm của phương trình \(f\left( x \right) = f\left( {\left| t \right|} \right)\)
Từ đó suy ra điều kiện có nghiệm của phương trình đã cho.
Chú ý rằng nếu hàm \(f\left( t \right)\) đồng biến (hoặc nghịch biến) trên \(\left( {a;b} \right)\) thì phương trình \(f\left( u \right) = f\left( v \right)\) nếu có nghiệm thì đó là nghiệm duy nhất trên \(\left( {a;b} \right) \Leftrightarrow u = v.\)
Vì \( - 1 \le \sin x \le 1; - 1 \le \cos x \le 1\) nên \(2\cos x - \sin x > - 3 \Rightarrow 2\cos x - \sin x + 4 > 0\)
Đặt \(\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}} = t \Leftrightarrow 3\sin x - \cos x - 1 = t\left( {2\cos x - \sin x + 4} \right)\)
\( \Leftrightarrow \cos x\left( {2t + 1} \right) - \sin x\left( {t + 3} \right) = - 4t - 1\)
Phương trình trên có nghiệm khi \({\left( {2t + 1} \right)^2} + {\left( {t + 3} \right)^2} \ge {\left( { - 4t - 1} \right)^2}\)
\( \Leftrightarrow 5{t^2} + 10t + 10 \ge 16{t^2} + 8t + 1\) \( \Leftrightarrow 11{t^2} - 2t - 9 \le 0 \Leftrightarrow - \dfrac{9}{{11}} \le t \le 1 \Rightarrow 0 \le \left| t \right| \le 1\)
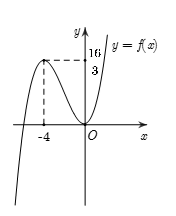
Từ đồ thị hàm số ta thấy hàm số \(f\left( x \right)\) đồng biến trên \(\left( {0;1} \right)\)
Nên phương trình \(f\left( x \right) = f\left( {\left| t \right|} \right)\) với \(t \in \left[ {0;1} \right]\) có nghiệm duy nhất khi \(x = \left| t \right| \Rightarrow 0 \le x \le 1\)
Do đó phương trình \(f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + m + 4} \right)\) có nghiệm
\( \Leftrightarrow \left| t \right| = {m^2} + 4m + 4\) có nghiệm với \(0 \le \left| t \right| \le 1\)
\( \Leftrightarrow 0 \le {m^2} + 4m + 4 \le 1 \Leftrightarrow {\left( {m + 2} \right)^2} \le 1 \Leftrightarrow - 3 \le m \le - 1\)
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 3; - 2; - 1} \right\}\). Vậy có 3 giá trị của \(m\) thỏa mãn yêu cầu.
Mình cần đánh giá cho biểu thức này em nhé :\(\left( {2\cos x - \sin x + 4} \right)\)
Mục đích đánh giá là để có thể quy đồng sau khi đặt t. Từ đó tìm điều kiện cho t.
Đáp án : D
Các bài tập cùng chuyên đề
Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:
Số giao điểm của đồ thị hàm số $y = {x^3} - 2{x^2} + x - 1$ và đường thẳng $y = 1 - 2x$ là:
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
Các đồ thị hàm số $y = {x^4} - 2{x^2} + 2$ và $y = - {x^2} + 4$ có tất cả bao nhiêu điểm chung?
Số giao điểm của hai đồ thị hàm số $y = 3{x^2}$ và $y = {x^3} + {x^2} + x + 1$ là:
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Cho hàm số $y = {x^3} + 3{x^2} + m$ có đồ thị $\left( C \right)$.Để đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm $A,B,C$ sao cho $C$ là trung điểm của $AB$ thì giá trị của tham số $m$ là:
Biết đường thẳng $y = mx + 1$ cắt đồ thị hàm số $y = {x^3} - 3x + 1$ tại ba điểm phân biệt. Tất cả các giá trị thực của tham số $m$ là:
Cho hàm số $y = {x^3} - \left( {m + 3} \right){x^2} + \left( {2m - 1} \right)x + 3\left( {m + 1} \right)$. Tập hợp tất cả các giá trị của $m$ để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là:
Tìm $m$ để đồ thị hàm số $y = {x^3} - 3{x^2} + 2$ cắt đường thẳng $y = m\left( {x - 1} \right)$ tại ba điểm phân biệt có hoành độ ${x_1},{x_2},{x_3}$ thỏa mãn $x_1^2 + x_2^2 + x_3^2 = 5$.
Tìm điều kiện của $m$ để đồ thị hàm số $\left( {{C_m}} \right):y = {x^4} - m{x^2} + m - 1$ cắt trục hoành tại $4$ điểm phân biệt.
Cho hàm số $y = {x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2}$$\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số $\left( 1 \right)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ ${x_1},{x_2},{x_3},{x_4}$ thoả mãn ${x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 = 6$
Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
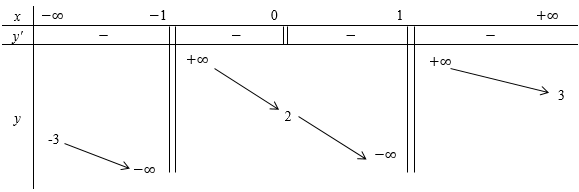
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
Cho hàm số $y = {x^4} - 4{x^2} + 3$. Tìm tất cả các giá trị của tham số $m$ sao cho phương trình $\left| {{x^4} - 4{x^2} + 3} \right| = m$ có $4$ nghiệm phân biệt.
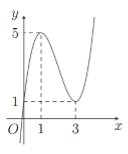
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right) = 3\) là:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau
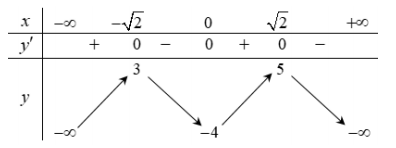
Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( {\sin x - \cos x} \right) = m - 1\) có hai nghiệm
phân biệt trên khoảng \(\left( { - \dfrac{\pi }{4};\dfrac{{3\pi }}{4}} \right)?\)
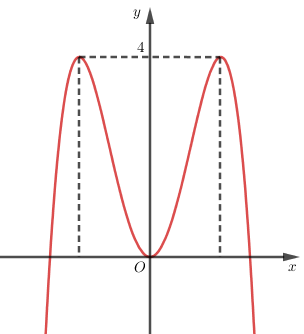
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt.
Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)
Cho hàm số bậc ba \(y = f\left( x \right)\) có bảng biến thiên trong hình dưới:
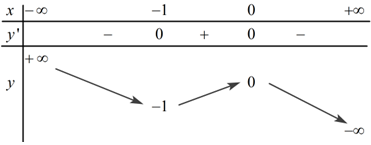
Số nghiệm của phương trình \(f\left( x \right) = - 0,5\) là:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.
