Cho hai số thực x,y thỏa mãn x2+y2−4x+6y+4+√y2+6y+10=√6+4x−x2. Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T=|√x2+y2−a|. Có bao nhiêu giá trị nguyên thuộc đoạn [−10;10] của tham số a để M≥2m?
-
A.
17.
-
B.
16.
-
C.
15.
-
D.
18.
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M(x;y)∈(C) để |OM−a| lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Ta có x2+y2−4x+6y+4+√y2+6y+10=√6+4x−x2
⇔x2+y2−4x+6y+4+√y2+6y+10−√6+4x−x2=0⇔x2+y2−4x+6y+4+(√y2+6y+10−√6+4x−x2)(√y2+6y+10+√6+4x−x2)√y2+6y+10+√6+4x−x2=0
⇔x2+y2−4x+6y+4+y2+6y+10−6−4x+x2√y2+6y+10+√6+4x−x2=0⇔x2+y2−4x+6y+4+x2+y2−4x+6y+4√y2+6y+10+√6+4x−x2=0
⇔(x2+y2−4x+6y+4)(1+1√y2+6y+10+√6+4x−x2)=0
⇔x2+y2−4x+6y+4=0 (vì 1+1√y2+6y+10+√6+4x−x2>0 )
⇔(x−2)2+(y+3)2=9
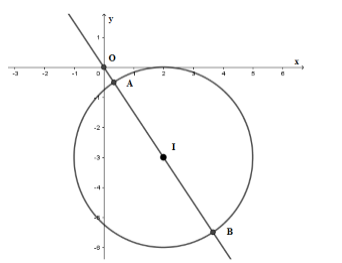
Phương trình (x−2)2+(y+3)2=9 là phương trình đường tròn (C) tâm I(2;−3) và bán kính R=3.
Gọi N(x;y)∈(C) ta suy ra ON=√x2+y2 suy ra T=|ON−a|
Gọi A,B là giao điểm của đường tròn (C) và đường thẳng OI.
Khi đó OA=OI−R=√13−3 và OB=OI+R=√13+3
Suy ra √13−3≤√x2+y2≤√13+3
TH1: Nếu √13−3≤a≤√13+3 thì |√x2+y2−a|≥0⇒minT=0⇒M≥2m⇒a∈{1;2;3;4;5;6}
TH2: Nếu a<√13−3⇒a<√13 nên |√13+3−a|>|√13−3−a|, do đó M=|√13+3−a|;m=|√13−3−a|
Vì M≥2m⇒|√13+3−a|≥2|√13−3−a|
⇔(√13+3−a)2−(2√13−6−2a)2≥0⇔√13−9≤a≤√13−1⇒a∈{−5;−4;−3;−2;−1;0}
TH3: Nếu a>√13+3⇒a>√13 nên |√13+3−a|<|√13−3−a|, do đó m=|√13+3−a|;M=|√13−3−a|
Vì M≥2m⇒|√13−3−a|≥2|√13+3−a|
⇔(√13−3−a)2−(2√13+6−2a)2≥0⇔√13+1≤a≤√13+9⇒a∈{7;8;9;10}
Vậy có 16 giá trị của a thỏa mãn đề bài.
Đáp án : B

Các bài tập cùng chuyên đề
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=sinx trên đoạn [−π2;−π3] lần lượt là
Cho biết GTLN của hàm số f(x) trên [1;3] là M=−2. Chọn khẳng định đúng:
Cho hàm số f(x) xác định trên [0;2] và có GTNN trên đoạn đó bằng 5. Chọn kết luận đúng:
Giá trị nhỏ nhất của hàm số y=2x+cosx trên đoạn [0;1] là :
Cho hàm số f(x) xác định và liên tục trên R, có limx→+∞f(x)=+∞;limx→−∞f(x)=−∞ , khi đó:
Gọi m là giá trị nhỏ nhất của hàm số y=x−1+4x−1 trên khoảng (1;+∞). Tìm m?
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, chọn kết luận đúng:
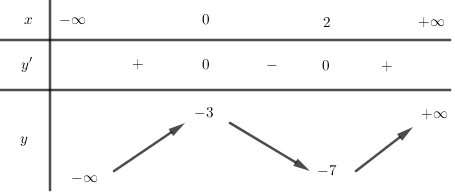
Cho hàm số y=f(x) có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
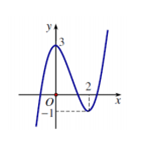
Cho hàm số y=f(x) có bảng biến thiên như sau:
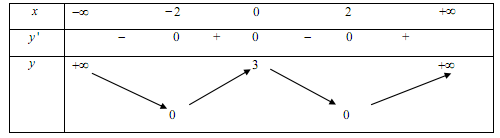
Khẳng định nào sau đây là khẳng định đúng?
Tìm giá trị lớn nhất của hàm số y=x3−5x2+3x−1 trên đoạn [2;4]
Tìm GTLN và GTNN của hàm số y=x5−5x4+5x3+1 trên đoạn [−1;2]
Giá trị lớn nhất của hàm số f(x)=6−8xx2+1 trên tập xác định của nó là:
Gọi giá trị lớn nhất và nhỏ nhất của hàm số y=x4+2x2−1 trên đoạn [−1;2] lần lượt là M và m. Khi đó giá trị của M.m là:
Cho hàm số y=x+1x. Giá trị nhỏ nhất của hàm số trên khoảng (0;+∞) là:
Cho hàm số y=2mx+1m−x. Giá trị lớn nhất của hàm số trên [2;3] bằng −13 khi m bằng:
Cho hàm số y=x3−3mx2+6, giá trị nhỏ nhất của hàm số trên [0;3] bằng 2 khi:
Cho các số thực x,y thỏa mãn (x−4)2+(y−4)2+2xy⩽ Giá trị nhỏ nhất m của biểu thức A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right) là:
Có bao nhiêu số nguyên m \in \left[ { - 5;5} \right] để \mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2.
Cho f\left( x \right) mà đồ thị hàm số y = f'\left( x \right) như hình vẽ bên
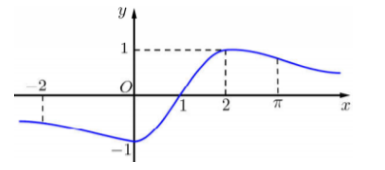
Bất phương trình f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m nghiệm đúng với mọi x \in \left[ { - 1;3} \right] khi và chỉ khi:
Cho hàm số y = f\left( x \right) xác định và liên tục trên \mathbb{R}, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f\left( x \right) trên đoạn \left[ { - 2;2} \right].