Cho tứ giác \(ABCD\) có \(\widehat A = \widehat D = {90^0},\widehat C = {45^0},AB = 6cm,AD = 8cm.\) Tính diện tích tứ giác \(ABCD.\)
-
A.
\(60\,\,c{m^2}\)
-
B.
\(80\,\,c{m^2}\)
-
C.
\(40\,\,c{m^2}\)
-
D.
\(160\,\,c{m^2}\)
+) Kẻ đường cao \(BE\)
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp để tính \(EC\).
+) Sử dụng công thức tính diện tích hình thang
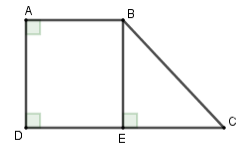
Vì \(\widehat A = \widehat D = {90^0} \Rightarrow AD{\rm{//}}BC\) hay \(ABCD\) là hình thang vuông tại \(A,D\)
Kẻ \(BE \bot DC\) tại \(E\).
Tứ giác \(ABED\) có ba góc vuông \(\widehat A = \widehat D = \widehat E = 90^\circ \) nên \(ABED\) là hình chữ nhật
Suy ra \(DE = AB = 6\,\,cm;BE = AD = 8\,cm\)
Xét tam giác \(BEC\) vuông tại \(E\) có \(\widehat {BCE} = 45^\circ \) nên tam giác \(BEC\) vuông cân tại \(E\) \( \Rightarrow EC = BE = 8cm \Rightarrow DC = DE + EC = 6 + 8 = 14cm\)
Do đó \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2} = \dfrac{{\left( {6 + 14} \right)8}}{2} = 80\,\,c{m^2}\).
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác $ABC$ vuông tại $A$ có \(AB = 5\,cm,\,\,\cot C = \dfrac{7}{8}\) . Tính độ dài các đoạn thẳng $AC$ và $BC$ . (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$AC \approx 4,39 (cm);BC \approx 6,66 (cm)$
-
B.
$AC \approx 4,38(cm);BC \approx 6,64(cm)$
-
C.
$AC \approx 4,38(cm);BC \approx 6,67(cm)$
-
D.
$AC \approx 4,37(cm);BC \approx 6,67(cm)$
Bài 2 :
Cho tứ giác $ABCD$ có $\widehat A = \widehat D = {90^0},\widehat C = {40^0},AB = 4cm,AD = 3cm.$ Tính diện tích tứ giác $ABCD.$ (làm tròn đến chữ số thập phân thứ hai)
-
A.
$17,36\,\,c{m^2}$
-
B.
$17,4\,\,c{m^2}$
-
C.
$17,58\,\,c{m^2}$
-
D.
$17,54\,\,c{m^2}$
Bài 3 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\,cm,\,\,\tan C = \dfrac{5}{4}\) . Tính độ dài các đoạn thẳng \(AC\) và \(BC\) . (làm tròn đến chữ số thập phân thứ \(2\) )
-
A.
\(AC = 11,53;BC = 7,2.\)
-
B.
\(AC = 7;BC \approx 11,53.\)
-
C.
\(AC = 5,2;BC \approx 11.\)
-
D.
\(AC = 7,2;BC \approx 11,53.\)
Bài 4 :
Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.
-
A.
\(\angle A = {45^0}\,\,;\,\,\,\angle B = \angle C = {67^0}30'\)
-
B.
\(\angle A = {30^0}\,\,;\,\,\,\angle B = \angle C = {75^0}\)
-
C.
\(\angle A = {48^0}6'\,\,;\,\,\,\angle B = \angle C = {65^0}57'\)
-
D.
\(\angle A = {53^0}8'\,\,;\,\,\,\angle B = \angle C = {63^0}26'\)
Bài 5 :
Cho tam giác \(ABC\) vuông cân tại \(A\left( {AB = AC = a} \right)\) . Phân giác của góc \(B\) cắt \(AC\) tại \(D\).
Tính \(DA;DC\) theo \(a\).
-
A.
\(AD = a.\cos 22,{5^0}\,\,;\,\,DC = a - a.\cos 22,{5^0}\)
-
B.
\(AD = a.\sin 22,{5^0}\,\,;\,\,DC = a - a.\sin 22,{5^0}\)
-
C.
\(AD = a.\tan 22,{5^0}\,\,;\,\,DC = a - a.\tan 22,{5^0}\)
-
D.
\(AD = a.\cot 22,{5^0}\,\,;\,\,DC = a - a.cot22,{5^0}\)
Bài 6 :
Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)
-
A.
\({S_{ABCD}} = 2\,\,\,\left( {đvdt} \right)\)
-
B.
\({S_{ABCD}} = 3\,\,\,\left( {đvdt} \right)\)
-
C.
\({S_{ABCD}} = 4\,\,\,\left( {đvdt} \right)\)
-
D.
\({S_{ABCD}} = \dfrac{5}{2}\,\,\,\left( {đvdt} \right)\)
Bài 7 :
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) (\(H\) thuộc \(BC\)). Biết \(\angle ACB = {60^0},\,\,CH = a\). Tính độ dài \(AB\) và \(AC\) theo \(a\).
-
A.
\(\begin{array}{l}AB = 2\sqrt 3 a\\AC = 2a\end{array}\)
-
B.
\(\begin{array}{l}AB = \sqrt 3 a\\AC = \dfrac{1}{2}a\end{array}\)
-
C.
\(\begin{array}{l}AB = a\\AC = 3a\end{array}\)
-
D.
\(\begin{array}{l}AB = \sqrt 3 a\\AC = a\end{array}\)
Bài 8 :
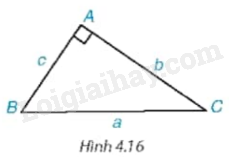
Xét tam giác ABC trong Hình 4.16.
a) Viết các tỉ số lượng giác tang, cotang của góc B và góc C theo b và c.
b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.
Bài 9 :
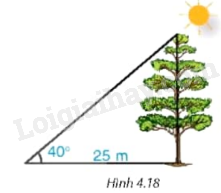
Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm) , biết rằng tia nắng mặt trời tạo với mặt đất góc \({40^0}\) (H.4.18).
Bài 10 :
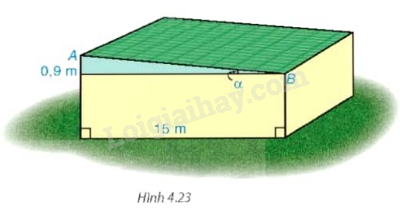
Tính góc nghiêng \(\alpha \) và chiều rộng AB của mái nhà kho trong Hình 4.23 (góc làm tròn đến độ, độ dài làm tròn đến dm)
Bài 11 :
Tính các góc của hình thoi có hai đường chéo dài \(2\sqrt 3 \) và 2.
Bài 12 :
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).
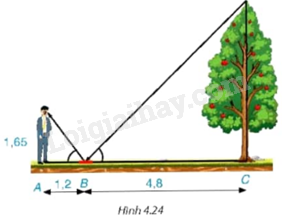
Bài 13 :
Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m) .
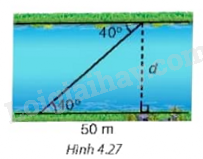
Bài 14 :
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc \({20^0}\) và chắn ngang lối đi một đoạn 5 m (H.4.36). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
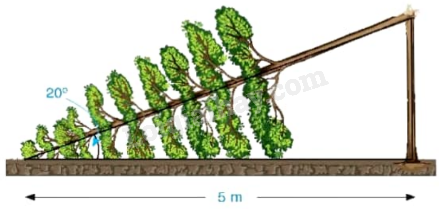
Bài 15 :
Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).
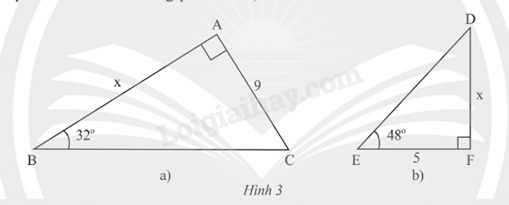
Bài 16 :
Cho tam giác MNP có \(\widehat N = {70^o},\widehat P = {38^o}\), đường cao MI = 11,5 cm. Độ dài cạnh NP của tam giác MNP (kết quả làm tròn đến hàng phần mười) bằng
A. 20,9 cm
B. 18,9 cm
C. 40,6 cm
D. 16,9 cm
Bài 17 :
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 17)
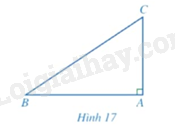
a) Biểu diễn \(\tan B,\cot C\) theo \(AB,AC\).
b) Viết công thức tính \(AC\) theo \(AB\) và \(\tan B\).
c) Viết công thức tính \(AC\) theo \(AB\) và \(\cot C\).
Bài 18 :
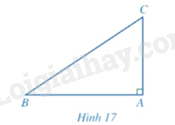
Tính \(AB\) trong Hình 17 khi \(AC = 4cm\) và \(\widehat B = 34^\circ \) (làm tròn kết quả đến hàng phần mười của centimét).
Bài 19 :
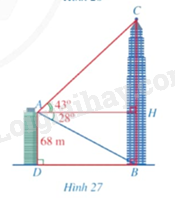
Từ vị trí \(A\) ở phía trên một tòa nhà có chiều cao \(AD = 68m\), bác Duy nhìn thấy vị trí \(C\) cao nhất của một tháp truyền hình, góc tạo bởi tia \(AC\) và tia \(AH\) theo phương nằm ngang là \(\widehat {CAH} = 43^\circ \). Bác Duy cũng nhìn thấy chân tháp tại vị trí \(B\) mà góc tạo bởi tia \(AB\) và tia \(AH\) là \(\widehat {BAH} = 28^\circ \), điểm \(H\) thuộc đoạn \(BC\) (Hình 27). Tính khoảng cách \(BD\) từ chân tháp đến chân tòa nhà và chiều cao \(BC\) của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).
Bài 20 :
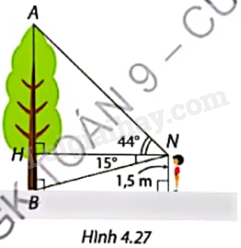
Quan sát Hình 4.27 và tính:
a) Khoảng cách NH giữa Nam và cây;
b) Chiều cao AB của cây.
Bài 21 :
Tính cạnh AC của tam giác vuông trong Hình 7.
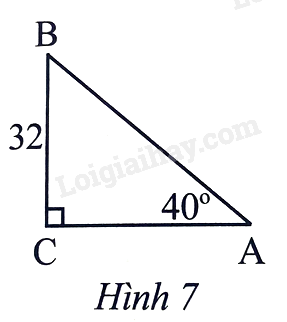
Bài 22 :
Cho tam giác ABC có AB = 6cm, \(\widehat A = 15^\circ ,\widehat B = 35^\circ \). Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet).
Bài 23 :
Cho tam giác ABC có \(BC = 11cm,\widehat {ABC} = {38^o},\widehat {ACB} = {30^o}\). Gọi H là chân đường vuông góc kẻ từ A đến BC. Hãy tính AH.
Bài 24 :
Chiều cao từ mặt đất đến đỉnh tháp Pisa ở Italia là 58m, tháp nghiêng góc \({5^o}30'\) đối với phương thẳng đứng (H.4.17). Khi Mặt Trời chiếu vuông góc với mặt đất thì bóng của tháp dài bao nhiêu decimét?

Bài 25 :
Cho tam giác ABC có đường cao AH, \(\widehat B = {60^o},\widehat C = {45^o}\) và cạnh \(BC = 6cm\). Chứng minh rằng \(AH = 3\left( {3 - \sqrt 3 } \right)cm\).
Bài 26 :
Hai chiếc thuyền A và B ở vị trí được minh họa như trong Hình 4.20. Tính khoảng cách giữa chúng (làm tròn đến m), biết \(IK = 380m\).
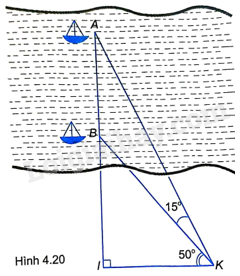
Bài 27 :
Độ dài y trong Hình 4 (kết quả làm tròn đến hàng phần mười) là
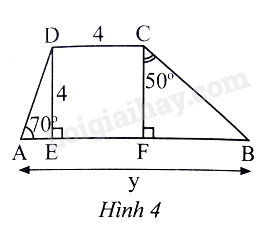
A. 10,2
B. 8,4
C. 10,3
D. 11
Bài 28 :
Từ một máy bay trực thăng, một người đặt mắt tại vị trí M ở độ cao MH = 920 m. Người đó nhìn hai vị trí A và B của hai đầu một cây cầu theo phương MA và MB tạo với phương nằm ngang Mx các góc lần lượt là \(\widehat {AMx} = 37^\circ ,\widehat {BMx} = 31^\circ \) với Mx // AB (Hình 24). Hỏi độ dài AB của cây cầu là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
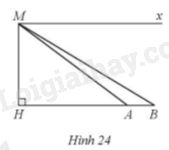
Bài 29 :
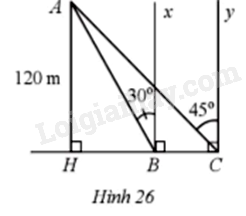
Flycam là từ viết tắt của Fly camera. Đây là thiết bị bay không người lái có lắp camera hay máy ảnh để quay phim hoặc chụp ảnh từ trên cao. Một chiếc Flycam đang ở vị trí A cách cây cầu BC (theo phương thẳng đứng) một khoảng AH = 120m. Biết góc tạo bởi phương AB, AC với các phương vuông góc với mặt cầu tại B, C lần lượt là \(\widehat {ABx} = 30^\circ ,\widehat {ACx} = 45^\circ \) (hình 26). Tính độ dài BC của cây cầu (làm tròn kết quả đến hàng phần trăm của mét).
Bài 30 :
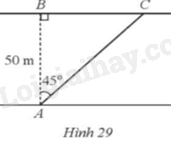
Một con sông có bề rộng AB = 50 m. Một chiếc thuyền đi thẳng từ vị trí A bên này bờ sông đến vị trí C bên kia bờ sông với góc tạo bởi phương AC và phương AB là \(\widehat {BAC} = 45^\circ \)(Hình 29). Hỏi độ dài đoạn thẳng BC là bao nhiêu mét?


















Danh sách bình luận