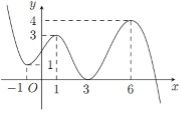
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Tìm số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).
-
A.
\(13\)
-
B.
$11$
-
C.
$10$
-
D.
$12$
Xác định số điểm mà đạo hàm đổi dấu của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).
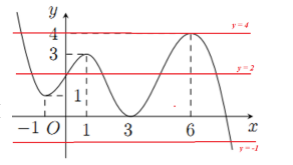
Ta có: \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}} \Rightarrow y' = {2019^{f\left( {f\left( x \right) - 1} \right)}}.f'\left( {f\left( x \right) - 1} \right).f'\left( x \right)\ln 2019\)
\(f'\left( {f\left( x \right) - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) - 1 = - 1\\f\left( x \right) - 1 = 1\\f\left( x \right) - 1 = 3\\f\left( x \right) - 1 = 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f\left( x \right) = 2\\f\left( x \right) = 4\\f\left( x \right) = 7\end{array} \right.\)
\(f'\left( {f\left( x \right) - 1} \right) = 0\) có tất cả: \(2 + 5 + 2 + 1 = 10\) nghiệm
(trong đó, có các nghiệm \(x = 3,\,\,x = 6\) là nghiệm kép, còn lại là nghiệm đơn).
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 3\\x = 6\end{array} \right.\) : có 4 nghiệm
\( \Rightarrow y' = {2019^{f\left( {f\left( x \right) - 1} \right)}}.f'\left( {f\left( x \right) - 1} \right).f'\left( x \right) = 0\) có 12 nghiệm phân biệt, trong đó, \(x = 3,\,\,x = 6\) là nghiệm bội 3, còn lại là nghiệm đơn.
Do đó, số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\) là 12.
Đáp án : D

Các bài tập cùng chuyên đề
Bài 1 :
Bất phương trình $\sqrt {2{x^3} + 3{x^2} + 6x + 16} - \sqrt {4 - x} \geqslant 2\sqrt 3 $ có tập nghiệm là $\left[ {a;b} \right].$ Hỏi tổng $a + b$ có giá trị là bao nhiêu?
-
A.
$5$
-
B.
$ - 2$
-
C.
$4$
-
D.
$3$
Bài 2 :
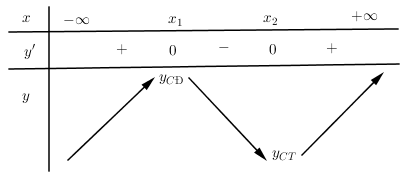
Hàm đa thức bậc ba không có cực trị và nghịch biến có bảng biến thiên dạng nào dưới đây?
-
A.
-
B.
-
C.
-
D.
Bài 3 :
Hàm đa thức bậc ba đồng biến trên \(\mathbb{R}\) có thể có bảng biến thiên dạng nào dưới đây?
-
A.

-
B.

-
C.

-
D.

Bài 4 :
Cho phương trình \({x^3} + \left( {m - 12} \right)\sqrt {4x - m} = 4x\left( {\sqrt {4x - m} - 3} \right)\), với \(m\) là tham số. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm thực phân biệt?
-
A.
$3$
-
B.
$4$
-
C.
$2$
-
D.
$1$
Bài 5 :
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 2019;\,2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;\, - 1} \right)\)?
-
A.
\(2010\).
-
B.
\(2012\).
-
C.
\(2011\).
-
D.
\(2009\).
Bài 6 :
Cho bất phương trình \(\sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^2}\left( {{x^2} - 1} \right) > 1 - m\). Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình nghiệm đúng với mọi \(x > 1.\)
-
A.
\(m \ge \dfrac{1}{2}\)
-
B.
\(m > 1\)
-
C.
\(m > \dfrac{1}{2}\)
-
D.
\(m \ge 1\)
Bài 7 :
Cho hàm số đa thức \(f(x)\) có đạo hàm tràm trên \(R\). Biết \(f(0) = 0\) và đồ thị hàm số \(y = f'\left( x \right)\) như hình sau.
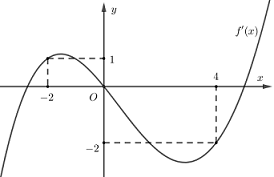
Hàm số \(g(x) = \left| {4f(x) + {x^2}} \right|\) đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( {4; + \infty } \right)\).
-
B.
\(\left( {0;4} \right)\).
-
C.
\(\left( { - \infty ; - 2} \right)\).
-
D.
\(\left( { - 2;0} \right)\).
Bài 8 :
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\), có đồ thị \(f\left( x \right)\) như hình vẽ. Hàm số \(g\left( x \right) = f\left( {{x^3} + x} \right)\) đạt cực tiểu tại điểm \({x_0}\). Giá trị \({x_0}\) thuộc khoảng nào sau đây?
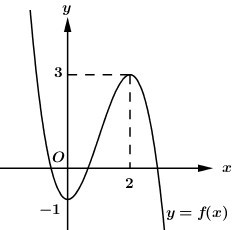
-
A.
\(\left( {1;3} \right)\)
-
B.
\(\left( {0;2} \right)\)
-
C.
\(\left( {-1;1} \right)\)
-
D.
\(\left( {3; + \infty } \right)\)
Bài 9 :
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \(f'\left( x \right)\) như hình vẽ bên. Số điểm cực đại của hàm số \(g\left( x \right) = f\left( { - {x^2} + x} \right)\) là:
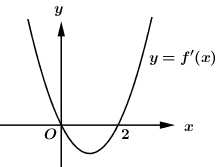
-
A.
\(2\)
-
B.
\(4\)
-
C.
\(5\)
-
D.
\(3\)
Bài 10 :
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 1 \right) = 1\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Có bao nhiêu số nguyên dương a để hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - a} \right|\) nghịch biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\)?
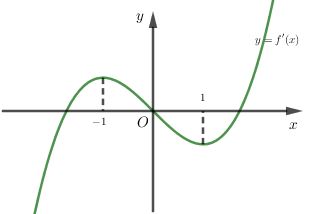
-
A.
\(2\)
-
B.
\(3\)
-
C.
Vô số
-
D.
\(5\)
Bài 11 :
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hàm số \(y = f\left( {{x^2} + 4x} \right) - {x^2} - 4x\) có bao nhiêu điểm cực trị thuộc khoảng \(\left( { - 5;1} \right)\)?
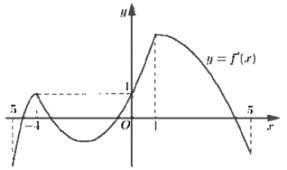
-
A.
\(5\)
-
B.
\(4\)
-
C.
\(6\)
-
D.
\(3\)
Bài 12 :
Số điểm cực trị của hàm số \(y = \left| {{x^2} - 3x + 2} \right|\) là:
-
A.
\(2\)
-
B.
\(3\)
-
C.
\(1\)
-
D.
\(4\)
Bài 13 :
Số điểm cực trị của hàm số \(y = \left| {\left( {x - 1} \right){{\left( {x - 2} \right)}^2}} \right|\) là:
-
A.
3
-
B.
1
-
C.
4
-
D.
2
Bài 14 :
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 3{x^2}} \right)\) là:
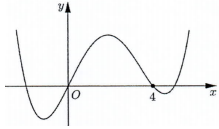
-
A.
\(5\)
-
B.
\(3\)
-
C.
\(7\)
-
D.
\(11\)
Bài 15 :
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên.

Hàm số \(y = f\left( {{x^2} - 1} \right)\) có bao nhiêu điểm cực trị?
-
A.
\(5\).
-
B.
\(7\).
-
C.
\(4\).
-
D.
\(3\).
Bài 16 :
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {x - 3} \right)\). Điểm cực đại của hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) là:
-
A.
\(x = 3\)
-
B.
\(x = 0\)
-
C.
\(x = 1\)
-
D.
\(x = - 1\)
Bài 17 :
Đề mẫu ĐGNL HN 2021
Hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^3} - \dfrac{{29}}{8}{x^2} + \dfrac{9}{4}x + \dfrac{3}{8}\), \(\forall x\, \in \,\mathbb{R}\). Gọi \(S\) là tập hợp các điểm cực tiểu của hàm số \(g\left( x \right) = f\left( {2x + 1} \right) - {x^3}.\) Tổng giá trị các phần tử của \(S\) bằng
-
A.
\(\dfrac{{ - 1}}{2}\)
-
B.
\(\dfrac{1}{2}\)
-
C.
\(2\)
-
D.
\(1\)
Bài 18 :
Cho hàm số f(x) có đạo hàm trên (a;b). Phát biểu nào sau đây là sai?
-
A.
\(f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)\) thì hàm số \(y = f\left( x \right)\) gọi là nghịch biến trên \(\left( {a;b} \right)\).
-
B.
\(f'\left( x \right) > 0,\forall x \in \left( {a;b} \right)\) thì hàm số \(y = f\left( x \right)\) gọi là đồng biến trên \(\left( {a;b} \right)\).
-
C.
Hàm số \(y = f\left( x \right)\) gọi là nghịch biến trên \(\left( {a;b} \right)\) khi và chỉ khi \(\forall {x_1};{x_2} \in \left( {a;b} \right):{x_1} > {x_2} \Leftrightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
-
D.
Hàm số \(y = f\left( x \right)\) gọi là nghịch biến trên \(\left( {a;b} \right)\) khi \(f'\left( x \right) > 0,\forall x \in \left( {a;b} \right)\).
Bài 19 :
Quan sát đồ thị của hàm số \(y = {x^2}\) (H.1.2)

a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?
Bài 20 :
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
a) Đồ thị hàm số \(y = {x^3} - \frac{3}{2}{x^2}\) (H.1.11);
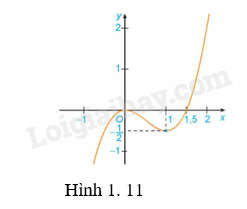
b) Đồ thị hàm số \(y = \sqrt[3]{{{{\left( {{x^2} - 4} \right)}^2}}}\) (H.1.12).

Bài 21 :
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?
A. Nếu \(f'\left( x \right) \ge 0\) với mọi x thuộc (a; b) thì hàm số \(y = f\left( x \right)\) đồng biến trên (a; b).
B. Nếu \(f'\left( x \right) > 0\) với mọi x thuộc (a; b) thì hàm số \(y = f\left( x \right)\) đồng biến trên (a; b).
C. Hàm số \(y = f\left( x \right)\) đồng biến trên (a; b) khi và chỉ khi \(f'\left( x \right) \ge 0\) với mọi x thuộc (a; b).
D. Hàm số \(y = f\left( x \right)\) đồng biến trên (a; b) khi và chỉ khi \(f'\left( x \right) > 0\) với mọi x thuộc (a; b).
Bài 22 :
Khoảng nghịch biến của hàm số \(y = {x^3} - 6{x^2} + 9x + 1\) là:
A. \(\left( { - \infty ;1} \right)\).
B. \(\left( {3; + \infty } \right)\).
C. \(\left( {1;3} \right)\).
D. \(\left( { - \infty ; + \infty } \right)\).
Bài 23 :
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập \(K \subset \mathbb{R}\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số \(y = f\left( x \right) = {x^2}\) có đồ thị như Hình 2.
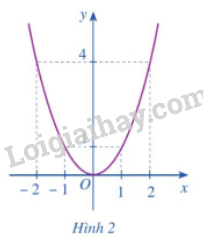
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.
- Xét dấu đạo hàm \(f'\left( x \right) = 2x\).
- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2}\) và dấu của đạo hàm \(f'\left( x \right) = 2x\) trên mỗi khoảng \(\left( { - \infty ;0} \right),\left( {0; + \infty } \right)\).
- Hoàn thành bảng biến thiên sau:
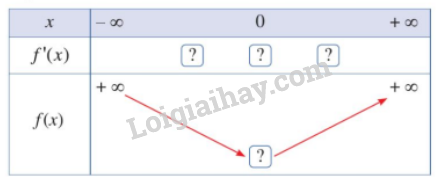
Bài 24 :
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng nào dưới đây?
A. \(\left( {1; + \infty } \right)\).
B. \(\left( { - 1;0} \right)\).
C. \(\left( { - 1;1} \right)\).
D. \(\left( {0;1} \right)\).
Bài 25 :
Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3.
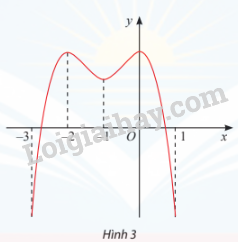
Bài 26 :
Cho hàm số y=f(x) có đạo hàm trên R và hàm số y=f’(x) có đồ thị như hình 31:

Hàm số y=f(x) đồng biến trên khoảng
a, \(\left( { - \infty ;0} \right) \)
b, \(\left( {0;1} \right)\)
c, \(\left( {0;2} \right)\)
d, \(\left( {1;2} \right) \)
Bài 27 :
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng
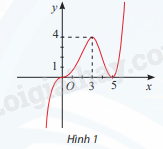
A. (5; \( + \infty \)). B. (3; 5). C. (0; 5). D. (3; \( + \infty \)).
Bài 28 :
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số đồng biến trên khoảng
-
A.
\(( - 1;1)\)
-
B.
\(( - \infty ; - 2)\)
-
C.
\((1; + \infty )\)
-
D.
\(( - 2;1)\)
Bài 29 :
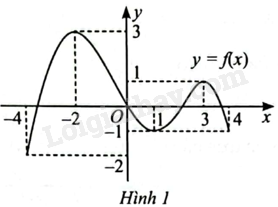
Hàm số \(y = f\left( x \right)\) trong Hình 1 nghịch biến trên khoảng nào?
A. \(\left( { - 2;1} \right)\).
B. \(\left( { - 4; - 2} \right)\).
C. \(\left( { - 1;3} \right)\).
D. \(\left( {1;3} \right)\).
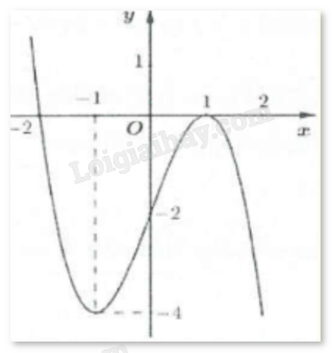
Bài 30 :
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào sau đây?
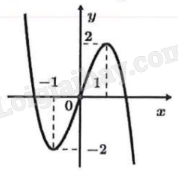
-
A.
\(( - \infty ; - 1)\)
-
B.
\(( - \infty ;1)\)
-
C.
\(( - 1;1)\)
-
D.
\((1; + \infty )\)


















Danh sách bình luận