Tam giác $ABC$ nằm trên đường tròn $\left( {O;R} \right)$ biết góc $\widehat C = {45^o}$ và $AB = a$. Bán kính đường tròn $\left( O \right)$ là
-
A.
\(a\sqrt 2 \)
-
B.
\(a\sqrt 3 \)
-
C.
\(\dfrac{{a\sqrt 2 }}{2}\)
-
D.
$\dfrac{{a\sqrt 3 }}{3}$
Sử dụng góc nội tiếp nhỏ hơn \(90^\circ \) có số đo bằng nửa số đo của góc ở tâm chắn cung đó.
Sử dụng định lí Pythagore để tính toán.

Xét đường tròn \(\left( O \right)\) có \(\widehat {ACB}\) là góc nội tiếp chắn cung \(AB\)
Mà \(\widehat {ACB} = {45^0}\) và \(\widehat {AOB} = {90^0}\) suy ra \(\Delta AOB\) vuông cân tại \(O\).
Theo định lí Pythagore ta có
$\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\2A{O^2} = A{B^2}\\AO = \dfrac{{a\sqrt 2 }}{2}\end{array}$
Vậy bán kính đường tròn là \(R = \dfrac{{a\sqrt 2 }}{2}\)
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
-
A.
\(AD.AE\)
-
B.
\(AD.AC\)
-
C.
\(AE.BE\)
-
D.
\(AD.BD\)
Bài 2 :
Cho \((O)\), đường kính \(AB\), điểm \(D\) thuộc đường tròn. Gọi \(E\) là điểm đối xứng với \(A\) qua \(D.\)
Bài 3 :
Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Khi đó tích $AB.AC$ bằng
-
A.
\(AH.HD\)
-
B.
$AH.AD$
-
C.
\(AH.HB\)
-
D.
$A{H^2}$
Bài 4 :
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
-
A.
\(13,5\,cm\)
-
B.
$12\,cm$
-
C.
\(18\,cm\)
-
D.
$6\,cm$
Bài 5 :
Cho hình vẽ (hai đường tròn có tâm là \(B,C \) và điểm \(B\) nằm trên đường tròn tâm \(C\)). Biết $\widehat {MAN} = {20^0}.$
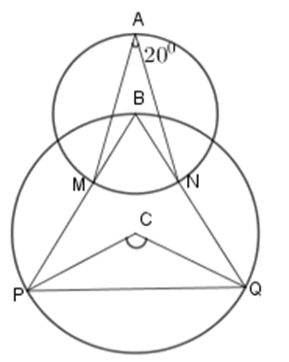
Khi đó \(\widehat {PCQ} = ?\)
-
A.
\({60^0}\)
-
B.
\({70^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Bài 6 :
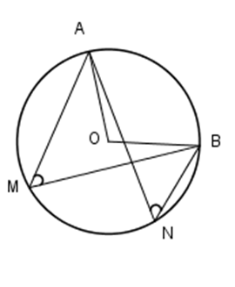
Cho hình vẽ bên. Mệnh đề nào sau đây là sai.
-
A.
\(\widehat {AMB} = \widehat {ANB}\)
-
B.
$\widehat {AMB} = \dfrac{1}{2}\widehat {AOB}$
-
C.
\(\widehat {ANB} = \dfrac{1}{2}\widehat {AOB}\)
-
D.
\(\widehat {AMB} = \widehat {ANB} = \widehat {AOB}\)
Bài 7 :
Cho đường tròn \(\left( O \right)\) Trên \(\left( O \right)\) lấy ba điểm \(A,B,D\) sao cho \(\widehat {AOB} = {120^0},\,\,AD = BD.\)
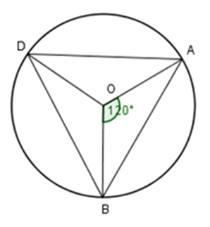
Khi đó \(\Delta ABD\) là:
-
A.
Tam giác đều.
-
B.
Tam giác vuông tại \(D\)
-
C.
Tam giác vuông cân tại \(D\)
-
D.
Tam giác vuông tại \(A\).
Bài 8 :
Cho bốn điểm A, B, C, D thuộc đường tròn \(\left( O \right).\) Biết \(\widehat {BOD} = {130^0}\) thì số đo \(\widehat {BAD}\) là:
-
A.
\({50^0}\)
-
B.
\({130^0}\)
-
C.
\({15^0}\)
-
D.
\({65^0}\)
Bài 9 :
Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Khi đó tứ giác \(ABEC\) là:
-
A.
Hình bình hành
-
B.
Hình thang
-
C.
Hình thang cân
-
D.
Hình thoi
Bài 10 :
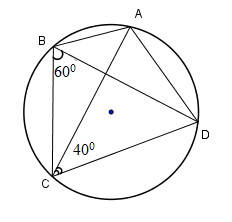
Cho hình vẽ. Khi đó đáp án đúng là
-
A.
\(\widehat {ADC} = {70^0}\)
-
B.
\(\widehat {ADC} = {80^0}\)
-
C.
\(\widehat {ADC} = {75^0}\)
-
D.
\(\widehat {ADC} = {60^0}\)
Bài 11 :
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(DA.DE\) bằng
-
A.
\(D{C^2}\)
-
B.
\(D{B^2}\)
-
C.
\(DB.DC\)
-
D.
\(AB.AC\)
Bài 12 :
Cho \((O)\), đường kính \(AB\), điểm \(D\) thuộc đường tròn sao cho \(\widehat {DAB} = 50^\circ \) . Gọi \(E\) là điểm đối xứng với \(A\)qua \(D.\)
Bài 13 :
Cho tam giác $ABC$ có \(AB = 5cm;AC = 3cm\) thuộc đường tròn tâm $(O),$ đường cao $AH$, đường kính $AD.$ Khi đó tích $AH.AD$ bằng
-
A.
\(15c{m^2}\)
-
B.
$8c{m^2}$
-
C.
\(12c{m^2}\)
-
D.
$30c{m^2}$
Bài 14 :
Cho tam giác $ABC$ nằm trên đường tròn $(O;R),$ đường cao $AH,$ biết $AB = 12{\rm{ }}cm,$$AC = 15{\rm{ }}cm,$ $AH = 6{\rm{ }}cm$.Tính đường kính của đường tròn $(O)$.
-
A.
\(13,5\,cm\)
-
B.
$12\,cm$
-
C.
\(15\,cm\)
-
D.
$30\,cm$
Bài 15 :
Hãy cho biết số đo góc nội tiếp tìm được trong Hình 9.3 ở Ví dụ 1, biết rằng số đo của các cung màu xanh trong hình đều bằng \({120^o}\).
Bài 16 :
Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng $\Delta AXC\backsim \Delta DXB$.
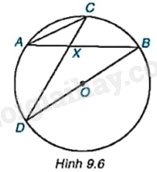
Bài 17 :
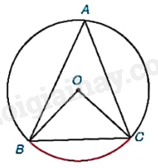
Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu đường tròn có bán kính 2cm và dây cung \(BC = 2\sqrt 2 cm\).
Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn.
Bài 18 :
Cho các điểm như Hình 9.7. Tính số đo các góc của tam giác ABC, biết rằng \(\widehat {AOB} = {120^o},\widehat {BOC} = {80^o}\).
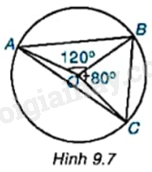
Bài 19 :
Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X (H.9.8). Tính số đo góc AXB biết rằng \(\widehat {ADB} = {30^o},\widehat {DBC} = {50^o}\).
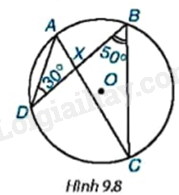
Bài 20 :
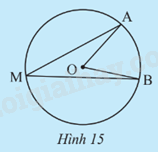
Quan sát Hình 15. Ta có góc nội tiếp \(\widehat {AMB}\) chắn cung AB trên đường tròn (O). Cho biết \(\widehat {AOB} = {60^o}\).
a) Tính số đo \(\overset\frown{AB}\).
b) Dùng thước đo góc để tìm số đo \(\widehat {AMB}\)
c) Có nhận xét gì về hai số đo của \(\widehat {AMB}\) và \(\overset\frown{AB}\).
Bài 21 :
Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho \(\widehat {AOB}\)= 50o; \(\widehat {BOC}\)= 30o, điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ \(\overset\frown{AB};\overset\frown{AC}\) và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:
a) \(\widehat {BCA};\widehat {BAC}\)
b) \(\widehat {MBA};\widehat {BAN}\)
Bài 22 :
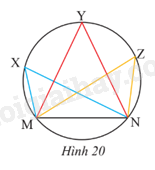
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì \(\widehat {MXN}\) gọi là góc sút từ vị trí X. Hãy so sánh các góc sút \(\widehat {MXN};\widehat {MYN};\widehat {MZN}\).
Bài 23 :
Góc nội tiếp chắn nửa đường tròn có số đo là:
A. 180o
B. 120o
C. 90o
D. 60o
Bài 24 :
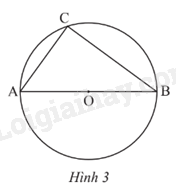
Trong Hình 3, \(\widehat {ACB}\) là góc
A. vuông
B. tù
C. nhọn
D. bẹt
Bài 25 :
Trong một đường tròn, khẳng định nào sau đây là sai?
A. Các góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Hai góc nội tiếp bằng nhau chắn hai cung bằng nhau.
C. Hai góc nội tiếp cùng chắn một cung thì bằng nhau.
D. Hai góc nội tiếp bằng nhau thì cùng chắn một cung.
Bài 26 :
Cho góc \(AIB\) nội tiếp đường tròn tâm \(O\) đường kính \(IK\) sao cho tâm \(O\) nằm trong góc đó (Hình 57).
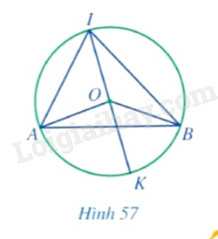
a) Các cặp góc \(\widehat {OAI}\) và \(\widehat {OIA};\widehat {OBI}\) và \(\widehat {OIB}\) có bằng nhau hay không?
b) Tính các tổng \(\widehat {AOI} + 2\widehat {OIA},\widehat {BOI} + 2\widehat {OIB}\).
c) Tính các tổng \(\widehat {AOI} + \widehat {AOK},\widehat {BOI} + \widehat {BOK}\).
d) So sánh \(\widehat {AOK}\) và \(2\widehat {OIA},\widehat {BOK}\) và \(2\widehat {OIB},\widehat {AOB}\) và \(2\widehat {AIB}\).
Bài 27 :
Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(AB = R\). Điểm \(C\) thuộc cung lớn \(AB,C\) khác \(A\) và \(B\). Tính số đo góc \(ACB\).
Bài 28 :
Quan sát Hình 60 và nêu mối liên hệ giữa
a) \(\widehat {AIB}\) và sđ$\overset\frown{AmB}$;
b) \(\widehat {AKB}\) và sđ$\overset\frown{AmB}$;
c) \(\widehat {AIB}\) và \(\widehat {AKB}\).
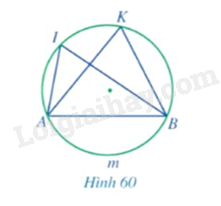
Bài 29 :
Trong Hình 61, gọi \(I\) là giao điểm của \(AD\) và \(BC\). Chứng minh \(IA.ID = IB.IC\).
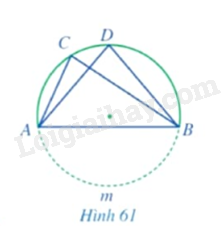
Bài 30 :
Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB\) sao cho \(\widehat {AOB} = 90^\circ \). Giả sử \(M,N\) lần lượt là các điểm thuộc cung lớn \(AB\) và cung nhỏ \(AB\) (\(M,N\) khác \(A\) và \(B\)).
a) Tính độ dài đoạn thẳng \(AB\) theo \(R\).
b) Tính số đo các góc \(ANB\) và \(AMB\).


















Danh sách bình luận