Gọi r và R lần lượt là bán kính đường tròn nội tiếp và ngoại tiếp của một tam giác đều. Tỉ số $\dfrac{r}{R}$ bằng:
-
A.
$\dfrac{1}{{\sqrt 3 }}$
-
B.
$\dfrac{{\sqrt 3 }}{2}$
-
C.
$\dfrac{1}{{\sqrt 2 }}$
-
D.
$\dfrac{1}{2}$
Sử dụng tỉ số lượng giác của góc nhọn để tính tỉ số cần thiết
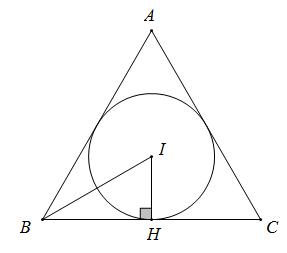
Giả sử tam giác đều ABC có đường tròn nội tiếp (I) tiếp xúc với BC tại H thì \(IH \bot BC\)
Vì ABC là tam giác đều nên I cũng là tâm đường tròn ngoại tiếp ∆ABC suy ra \( IH\) là trung trực BC
Do đó \(H\) là trung điểm BC
Vì I là tâm đường tròn nội tiếp tam giác nên BI là phân giác của $\widehat{ABC}$ nên $\widehat{IBH} = \dfrac{{\widehat{ ABC}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ $
Xét tam giác \(IHB\) ta có:
$\dfrac{r}{R} = \dfrac{{IH}}{{IB}} = \sin \widehat{ IBH} = \sin 30^\circ = \dfrac{1}{2}$
Đáp án : D

Các bài tập cùng chuyên đề
Bài 1 :
Cho đường tròn $\left( O \right)$ đường kính $AB$ . Gọi $H$ là điểm nằm giữa $O$ và $B$. Kẻ dây $CD$ vuông góc với $AB$ tại $H$ . Trên cung nhỏ $AC$ lấy điểm $E$ kẻ $CK$ vuông góc $AE$ tại $K$ . Đường thẳng $DE$ cắt $CK$ tại $F$. Chọn câu đúng:
-
A.
$AHCK$ là tứ giác nội tiếp.
-
B.
$AHCK$ không nội tiếp đường tròn.
-
C.
$\widehat {EAO} = \widehat {HCK}$
-
D.
$AH.AB = AD.BD.$
Bài 2 :
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {120^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy \(D\) sao cho \(BCD\) là tam giác đều. Khi đó
-
A.
\(\Delta ACD\) cân
-
B.
\(ABDC\) nội tiếp
-
C.
\(ABDC\) là hình thang
-
D.
\(ABDC\) là hình vuông
Bài 3 :
Cho điểm A nằm ngoài đường tròn (O) qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm) . Chọn đáp án đúng:
-
A.
Tứ giác ABOC là hình thoi
-
B.
Tứ giác ABOC nội tiếp
-
C.
Tứ giác ABOC không nội tiếp
-
D.
Tứ giác ABOC là hình bình hành.
Bài 4 :
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {130^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), kẻ \(Bx \bot BA;Cy \bot CA\), \(Bx\) và \(Cy\) cắt nhau tại D. Chọn đáp án sai.
-
A.
\(\Delta BCD\) cân
-
B.
\(ABDC\) nội tiếp
-
C.
\(ABDC\) là hình thoi
-
D.
\(\widehat {BDC} = 50^\circ \)
Bài 5 :
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số $\dfrac{R}{r}$ là:
-
A.
$\dfrac{1}{{\sqrt 2 }}$
-
B.
$2$
-
C.
$\dfrac{{\sqrt 3 }}{2}$
-
D.
đáp án khác
Bài 6 :
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng:
a) Tứ giác AEHF nội tiếp đường tròn tâm I;
b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Bài 7 :
Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông.
a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (C).
b) Gọi I và K lần lượt là trung điểm của các đường chéo AC và BD của tứ giác. Chứng minh rằng \(IK \bot BD\).
c) Kí hiệu các tiếp tuyến của đường tròn (C) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang.
d) Chứng minh rằng \(EF = AE + CF\).
Bài 8 :
Cho tam giác ABC \(\left( {AB < AC} \right)\) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng:
a) DBXF, DCYE là các tứ giác nội tiếp.
b) Bốn điểm X, Y, E, F thẳng hàng.
Bài 9 :
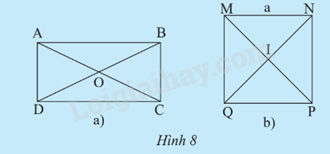
a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD.
b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
Bài 10 :
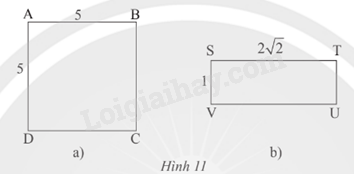
Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11.
Bài 11 :
Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp;
b) Các đường thẳng AB, MN, CD cùng đi qua một điểm.
Bài 12 :
Cho hình vuông ABCD có độ dài cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn thẳng BC tại M và tia Ay cắt đoạn thẳng CD kéo dài tại N.
a) Chứng minh hai tam giác ABM và ADN bằng nhau.
b) Gọi O là trung điểm của MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp.
c) Chứng minh ba điểm B, D, O thẳng hàng.
Bài 13 :
Cho tứ giác nội tiếp ABCD có hai đường chéo AC và BD cắt nhau tại I.
a) Hai góc ABD và ACD có bằng nhau hay không? Vì sao?
b) Chứng minh \(\Delta AIB\backsim \Delta IDC\) và IA.IC = IB.ID.
Bài 14 :
Cho tứ giác nội tiếp ABCD có hai tia CD và BA cắt nhau tại I. Chứng minh:
a)\(\widehat {IAD} = \widehat {BCD}.\)
b) IA.IB = ID.IC.
Bài 15 :
Giải thích vì sao giao điểm của hai đường chéo của hình chữ nhật và hình vuông cách đều bốn đỉnh của chúng.
Bài 16 :
Cho đường tròn tâm O có bán kính R = 5 cm.
a) Tính độ dài cạnh của hình vuông nội tiếp trong (O).
b) Một hình chữ nhật nội tiếp (O) có chu vi 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật đó.
Bài 17 :
Cho ABCD là tứ giác nội tiếp.
a) Chứng minh rằng \(\widehat {BAC} = \widehat {BDC}\).
b) AC cắt BD tại M. Chứng minh rằng MA.MC = MB.MD.
Bài 18 :
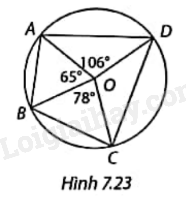
Tính số đo các góc của tứ giác nội tiếp ABCD trong Hình 7.23.
Bài 19 :
Tam giác ABC có \(\widehat B = {76^o},\widehat C = {40^o}\). Đường tròn (O) nội tiếp \(\Delta \)ABC tiếp xúc với các cạnh AB, BC, AC lần lượt tại các điểm M, N, P.
a) Chứng minh AMOP, BMON và CNOP là các tứ giác nội tiếp.
b) Tính số đo cung nhỏ MN, NP và MP.
c) Tính các góc của \(\Delta \)MNP.
Bài 20 :
Cho đường tròn (O) có hai đường kính AB và MN vuông góc với nhau. Trên tia đối của tia MA lấy điểm C khác điểm M. Gọi H là chân đường vuông góc kẻ từ điểm M đến đường thẳng BC.a) Chứng minh bốn điểm O, M, H, B cùng thuộc một đường tròn.
b) Hai đường thẳng MB và OH cắt nhau tại E. Chứng minh \(\angle MHO = \angle MNA\) và \(ME \cdot MH = BE \cdot HC\).
c) Gọi P là giao điểm thứ hai của đường tròn (O) và đường tròn ngoại tiếp tam giác MHC. Chứng minh ba điểm C, P, E là ba điểm thẳng hàng.
Bài 21 :
Cho tam giác ABC có ba góc nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt hai cạnh AB, AC lần lượt tại E và F (E khác B, F khác C). Các đoạn thẳng BF và CE cắt nhau tại H, tia AH cắt BC tại K.a) Chứng minh \(\angle BEC = \angle BFC = {90^0}\), từ đó suy ra tứ giác AEHF nội tiếp.
b) Gọi D là giao điểm của AH và (O) (D nằm giữa A và H), chứng minh \(B{D^2} = BK \cdot BC\) và \(\angle BDH = \angle BFD\)
c) Trong trường hợp góc \(BAC = {60^0}\) và \(BC = 6\;{\rm{cm}}\), tính độ dài đoạn thẳng EF và bán kính đường tròn ngoại tiếp tam giác AEF.
Bài 22 :
Cho tam giác ABC nhọn \((AB < AC)\) có đường cao AD và đường phân giác trong AO(D,O thuộc cạnh BC). Kẻ OM vuông góc với AB tại M, ON vuông góc với AC tại N.a) Chứng minh bốn điểm D,M,N,O cùng nằm trên một đường tròn.
b) Chứng minh \(OM = ON\) và \(\angle BDM = \angle ODN\).
c) Qua \(O\), kẻ đường thắng vuông góc với BC cắt MN tại I,AI cắt BC tại \(K\). Chứng minh \(K\) là trung điểm của BC.
Bài 23 :
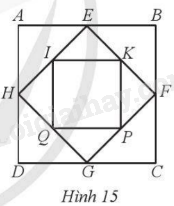
Hình vuông ABCD có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp của nó để tạo thành tứ giác EFGH, tiếp tục như vậy được tứ giác mới IKPQ (Hình 15). Chứng minh:
a) Tứ giác EFGH và tứ giác IKPQ là các tứ giác nội tiếp đường tròn.
b) Tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH bằng tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ.
Bài 24 :
Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh:
a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp.
b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.
Bài 25 :
Cho đường tròn tâm \((O)\) và dây \(BC\) cố định không đi qua \(O\). Trên cung lớn \(BC\) lấy điểm \(A\) sao cho \(AB < AC\). Kẻ đường kính \(AK,\,E\) là hình chiếu của \(C\) trên \(AK\). \(M\) là trung điểm của \(BC\).a) Chứng minh bốn \(C,\,E,\,\,M,\,O\) cùng thuộc một đường tròn.
b) Kẻ \(AD \bot BC\) tại \(D\). Chứng minh \(AD.AK = AB.AC\) và \(\Delta MDE\) cân.
c) Gọi \(F\) là hình chiếu của \(B\) trên \(AK\). Chứng minh khi di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.
Bài 26 :
Cho đường tròn \(\left( {O{\mkern 1mu} ;{\mkern 1mu} R} \right)\), đường kính AB vuông góc với dây CD tại điểm \(I\) (\(I\) nằm giữa \(A\) và \(O\)). Lấy điểm \(E\) bất kì trên cung nhỏ BC \((\)E khác \(B\) và \(C\)). AE cắt CD tại \(K\).a) Chứng minh bốn điểm K, E, B, I cùng thuộc một đường tròn.
b) Chứng minh \(AK.AE = AI.AB\).
c) Gọi \(P\) là giao điểm của tia BE và tia DC, \(Q\) là giao điểm của AP và BK. Chứng minh IK là phân giác của \(\widehat {EIQ}\). Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp tam giác PQE.
Bài 27 :
Cho tam giác ABC ba góc nhọn nội tiếp (O;R), hai đường cao BE, CF cắt nhau tại H.a) Chứng minh tứ giác BFCE nội tiếp và \(AO \bot EF\)
b) Chứng minh: \({\sin ^2}\widehat {BAC}{\mkern 1mu} + {\mkern 1mu} c{\rm{o}}{s^2}\widehat {BAC} = 1\) và \(B{C^2}{\mkern 1mu} = {\mkern 1mu} A{B^2}{\mkern 1mu} + {\mkern 1mu} A{C^2}{\mkern 1mu} - 2.AB.AC.cos\widehat {BAC}\)
c) Gọi S là diện tích tam giác ABC, chứng minh \(S = {\mkern 1mu} \frac{1}{2}AB.AC.\sin \widehat {BAC}\). Cho \(AB = 6;{\mkern 1mu} AC = 8;BC = 2\sqrt {13} \). Tính diện tích tam giác ABC.
Bài 28 :
Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm K, hai đường chéo AC và BD cắt nhau tại điểm H. Kí hiệu $\overset\frown{AD}$ là cung AD không chứa điểm B và $\overset\frown{BC}$ là cung BC không chứa A. Chứng minh rằng:
a) \(\widehat {BKC} = \frac{1}{2}\)(sđ$\overset\frown{AD}$ - sđ$\overset\frown{BC}$);
b) \(\widehat {BHC} = \frac{1}{2}\)(sđ$\overset\frown{AD}$ + sđ$\overset\frown{BC}$).
Bài 29 :
a) Nếu một hình bình hành nội tiếp một đường tròn thì hình đó phải là là hình chữ nhật;
b) Nếu một hình thoi nội tiếp một đường tròn thì hình đó phải là hình vuông;
c) Nếu một hình thang nội tiếp một đường tròn thì hình đó phải là hình thang cân.
Bài 30 :
Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB=3cm; AD=4cm. Vẽ một hình vuông nội tiếp (O). Tính diện tích của hình vuông đó.


















Danh sách bình luận