Tính diện tích tam giác đều nội tiếp đường tròn \(\left( {O;2cm} \right)\)
-
A.
\(6c{m^2}\)
-
B.
\(6\sqrt 3 c{m^2}\)
-
C.
\(3c{m^2}\)
-
D.
\(3\sqrt 3 c{m^2}\)
+ Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{\sqrt 3}{3}a\).
+ Sử dụng công thức tính diện tích tam giác \(S = \dfrac{{ah}}{2}\) với \(h\) là chiều cao ứng với cạnh đáy là \(a\)
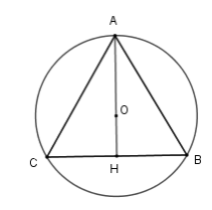
Gọi tam giác đều ABC nội tiếp \(\left( {O;2cm} \right)\) thì đường tròn \(\left( {O;2cm} \right)\) ngoại tiếp tam giác đều ABC.
Đường tròn ngoại tiếp tam giác đều cạnh a có bán kính bằng \(\frac{\sqrt 3}{3}a\) hay \(2 =\frac{\sqrt 3}{3}a\).
Suy ra \(a = 2:\frac{\sqrt 3}{3} = 2\sqrt 3\).
Gọi \(AH\) là đường trung tuyến của tam giác đều nên \(\dfrac{2}{3}AH = AO = 2cm\) suy ra \( AH = 2:\dfrac{2}{3} = 3cm\)
Diện tích tam giác \(ABC\) là:
\(S = \dfrac{1}{2}AH.BC = \dfrac{1}{2}3.2\sqrt 3 = 3\sqrt 3 \left( {c{m^2}} \right)\)
Đáp án : D
Một số em có thể thiếu hệ số \(\dfrac{1}{2}\) ở công thức diện tích dẫn đến chọn đáp án B sai.

Các bài tập cùng chuyên đề
Bài 1 :
Tính độ dài cạnh của tam giác đều nội tiếp \(\left( {O;R} \right)\) theo \(R.\)
-
A.
\(\dfrac{R}{{\sqrt 3 }}\)
-
B.
\(\sqrt 3 R\)
-
C.
\(R\sqrt 6 \)
-
D.
\(3R\)
Bài 2 :
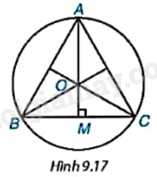
a) Vẽ tam giác đều ABC. Hãy trình bày cách xác định tâm của đường tròn ngoại tiếp tam giác ABC và vẽ đường tròn đó.
b) Giải thích vì sao tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó (H.9.17).
c) Giải thích vì sao \(\widehat {OBM} = {30^o}\) và \(OB = \frac{{\sqrt 3 }}{3}BC\) (với M là trung điểm của BC).
Bài 3 :
Cho tam giác đều ABC nội tiếp đường tròn (O) có bán kính bằng 4cm. Tính độ dài các cạnh của tam giác ABC.
Bài 4 :
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3cm. Tính diện tích tam giác ABC.
Bài 5 :
Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.26.
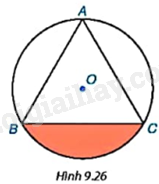
a) Tính bán kính R của đường tròn (O).
b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.
Bài 6 :
Trong một khu vui chơi có dạng hình tam giác đều có cạnh bằng 60m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa 50m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?
Bài 7 :
Một trại nuôi gia súc có dạng hình tam giác đều cạnh 100 m (Hình 12). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác. Nêu cách xác định vị trí đặt đèn và tính khoảng cách từ điểm đó đến ba đỉnh của tam giác.
Bài 8 :
Cho tam giác đều ABC nội tiếp đường tròn (O; 2cm). Tính AB.
Bài 9 :
Một chiếc máy quay ở đài truyền hình được đặt trên giá đỡ 3 chân, các điểm tiếp xúc với mặt đất của 3 chân lần lượt là 3 đỉnh A, B, C của tam giác đều ABC (Hình 16). Tính khoảng cách giữa 2 vị trí A và B, biết bán kính đường tròn ngoại tiếp tam giác ABC là 4 dm.

Bài 10 :
Biểu tượng tái chế trên thiết kế của huy hiệu hình tròn tam O được bạn Minh dựng dựa trên tam giác đều ABC nội tiếp trong (O) như Hình 7.10. Độ dài cạnh MN của biểu tượng tái chế bằng \(\frac{3}{5}\) độ dài BC. Tính MN nếu đường kính huy hiệu là 4 cm. Làm tròn kết quả đến hàng phần mười centimet.
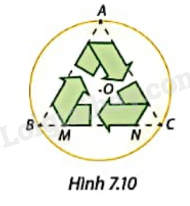
Bài 11 :
Bạn An sử dụng các hình viên phân như Hình 7.25a để ghép thành mẫu hoa văn trang trí như trong Hình 7.25b. Tính diện tích của mẫu hoa văn.
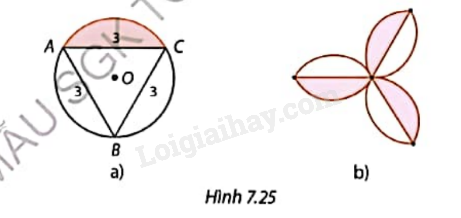
Bài 12 :
Trong một dân cư có dạng hình tam giác đều với cạnh bằng \(60m\), người ta muốn tìm một vị trí đặt bộ phát wifi công cộng sao cho ở chỗ nào trong khu dân cư đều có thể bắt được sóng. Hỏi để có thể bắt được sóng wifi ở mọi nơi trong khu dân cư thì tầm phát sóng của thiết bị tối đa sẽ là bao nhiêu m?
-
A.
\(20\sqrt 3 m\)
-
B.
\(20m\)
-
C.
\(50m\)
-
D.
\(50\sqrt 3 m\)
Bài 13 :
Tính chu vi của tam giác đều nội tiếp \(\left( {O\,;\,R} \right)\) theo R
-
A.
\(\frac{R}{{\sqrt 3 }}\)
-
B.
\(\sqrt 3 R\)
-
C.
\(R\sqrt 6 \)
-
D.
\(3\sqrt 3 R\)
Bài 14 :
Tính chu vi và diện tích của tam giác đều nội tiếp một đường tròn bán kính 3cm.
Bài 15 :
Cho một lục giác đều và một tam giác đều cùng nội tiếp một đường tròn. Biết rằng tam giác đều có cạnh bằng 3cm. Tính chu vi và diện tích của hình lục giác đều đã cho.
Bài 16 :
Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như hình bên.
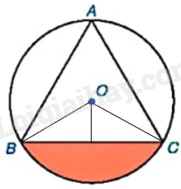
a) Tính bán kính R của đường tròn (O).
b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.
Bài 17 :
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2cm. Tính độ dài các cạnh của tam giác ABC.
Bài 18 :
Một chiếc máy quay ở đài truyền hình được đặt trên giá đỡ 3 chân, các điểm tiếp xúc với mặt đất của 3 chân lần lượt là 3 đỉnh A, B, C của tam giác đều ABC. Tính khoảng cách giữa hai vị trí A và B biết bán kính đường tròn ngoại tiếp tam giác ABC là 6dm.
Bài 19 :
Cẩu tháp là một loại thiết bị nâng hạ được thiết kế để nâng, hạ và di chuyền vật liệu xây dựng tại các công trường, đặc biệt là trong xây dựng các công trình cao tầng. Có khả năng hoạt động ở độ cao lớn và với tải trọng nặng, cẩu tháp được lắp đặt cố định hoặc có thể di chuyển trên ray tại công trường, giúp tăng hiệu quả công việc và đảm bảo an toàn lao động. Ba vị trí A, B, C của một công trình là ba đỉnh của một tam giác đều. Trên công trình, người ta muốn đặt cẩu tháp tại điểm O sao cho bán kính quay của cẩu tháp đến các vị trí điểm A, B, C bằng nhau và bằng 60 m (hình bên). Tính khoảng cách từ A đến B (làm tròn đến số hàng đơn vị).
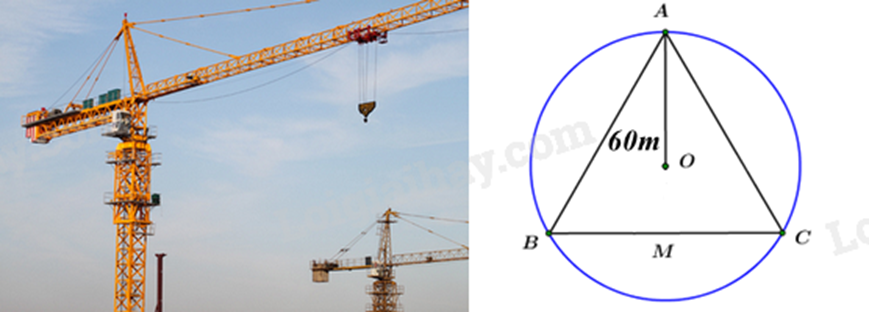


















Danh sách bình luận