Đề bài

Cho tam giác \(ABC\) không cân, nội tiếp đường tròn \(\left( O \right),\,\,BD\) là đường phân giác của góc \(\widehat {ABC}.\) Đường thẳng \(BD\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(E.\) Đường tròn \(\left( {{O_1}} \right)\) đường kính \(DE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Khi đó đường thẳng đối xứng với đường thẳng \(BF\) qua đường thẳng \(BD\) cắt \(AC\) tại \(N\) thì:

• A. \(AN = NC.\)
• B. \(AD = DN.\) 
• C. \(AN = 2NC.\)
• D. \(2AN = NC.\)

Phương pháp giải

Chứng minh \(N\) là trung điểm của \(AC\) bằng cách gọi \(M\) là trung diểm của \(AC\) rồi chứng minh \(\widehat {FBE} = \widehat {MBE}\), từ đó suy ra \(BM\) đối xứng với \(BF\) qua \(BE\).

Lời giải của GV Loigiaihay.com

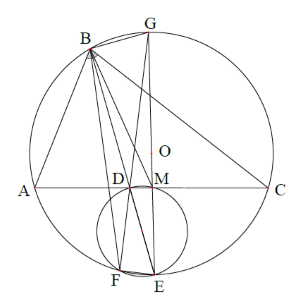
Gọi \(M\) là trung điểm của \(AC.\) Do \(E\) là điểm chính giữa cung \(AC\) nên \(EM \bot AC.\)

Do đó \(EM\) đi qua tâm của đường tròn \(\left( O \right).\) Giả sử rằng \(G = DF \cap \left( O \right).\) Do \(\widehat {DFE} = {90^0},\) nên

\(\widehat {GFE} = {90^0},\) hay \(GE\) là đường kính của \(\left( O \right).\) Suy ra \(G,M,E\) thẳng hàng.

Vì vậy \(\widehat {GBE} = {90^0},\) mà \(\widehat {GMD} = {90^0}.\)

Kéo theo tứ giác \(BDMG\) là tứ giác nội tiếp đường tròn đường kính \(GD.\)

Vì vậy \(\widehat {MBD} = \widehat {DGM} = \widehat {FGE}\,\,\left( 1 \right)\) (cùng chắn cung \(DM)\)

 Lại có tứ giác \(BFEG\) là tứ giác nội tiếp nên \(\widehat {FBE} = \widehat {FGE}\,\,\left( 2 \right)\,\) ( cùng chắn cung \(FE\) ).

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(\widehat {MBD} = \widehat {FBE}.\) Do đó \(BF\) và \(BM\) đối xứng nhau qua \(BD.\)

Vì vậy \(M \equiv N\) hay \(N\) là trung điểm của \(AC\) nên \(AN = NC.\)

Đáp án : A