Đề bài

Tứ giác ABCD nội tiếp (O) . Hai đường chéo AC và BD cắt nhau tại I. Vẽ đường tròn ngoại tiếp tam giác ABI. Tiếp tuyến của đường tròn này tại I cắt AD và BC lần lượt M và N. Chọn câu sai:

• A. MN // DC.      
• B. Tứ giác ABNM nội tiếp.
• C. Tứ giác MICD nội tiếp.                     
• D. Tứ giác INCD là hình thang

Phương pháp giải

Góc nội tiếp chắn nửa đường tròn là góc vuông.

Dấu hiệu nhận biết tứ giác nội tiếp:

+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)

+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)

+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.

+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.

Lời giải của GV Loigiaihay.com

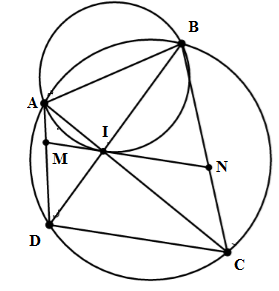
Xét đường tròn ngoại tiếp tam giác ABI ta có:

\(\widehat {BAI}\) là góc nội tiếp chắn cung BI.

\(\widehat {BIN}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BI.

\( \Rightarrow \widehat {BAI} = \widehat {BIN}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BI).

Xét đường tròn (O) ta có:

\(\widehat {BDC} = \widehat {BAC}\) (hai góc nội tiếp cùng chắn cung BC).

\( \Rightarrow \widehat {BIN} = \widehat {BDC}\left( { = \widehat {BAC}} \right)\)

Lại có hai góc này ở vị trí đồng vị

\( \Rightarrow IN//CD\;\;hay\;\;MN//CD\;\;\left( {dpcm} \right).\)

\( \Rightarrow \) đáp án A đúng.

Do MN//CD nên \(\widehat {MNC} + \widehat {NCD} = {180^0}\)(trong cùng phía)

Mà do tứ giác ABCD nội tiếp nên \(\widehat {MAB} + \widehat {NCD} = {180^0}\)

=> \(\widehat {MNC} = \widehat {NAB}\)

=> Tứ giác ABNM nội tiếp (góc trong bằng góc ngoài tại đỉnh đối diện)

\( \Rightarrow \) Đáp án B đúng.

+) Ta có: \(IN//CD\;\;\left( {cmt} \right) \Rightarrow \) INCD là hình thang \( \Rightarrow \) đáp án D đúng.

Đáp án : C