Đề bài

Đoạn mạch xoay chiều AB có RLC nối tiếp , cuộn dây thuần cảm với CR² < 2L; điện áp hai đầu đoạn mạch là u_AB = U√2cosωt, U ổn định và ω thay đổi . Khi ω = ω_C thì điện áp hai đầu tụ C cực đại, khi đó điện áp tức hai đầu đoạn mạch AN ( gồm RL ) và AB lệch pha nhau là α . Giá trị nhỏ nhất của a là : 

• A. 70,53⁰                   
• B. 90⁰
• C. 68,43⁰
• D. 120,3⁰

Phương pháp giải

Sử dụng công thức tính \(\tan (a - b) = \frac{{a - b}}{{1 + ab}}\)

Lời giải của GV Loigiaihay.com

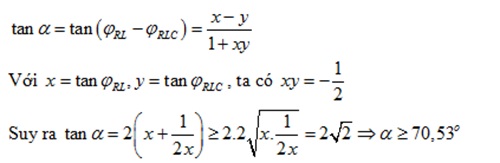
Đáp án : A