Đề bài

 Đoạn mạch xoay chiều RLC nối tiếp , cuộn dây thuần cảm với \(C{R^2} < {\rm{ }}2L\) ; điện áp hai đầu đoạn mạch là \(u = U\sqrt 2 cos\omega t\) , U ổn định và \(\omega \)  thay đổi . Khi \(\omega {\rm{ }} = {\rm{ }}{\omega _L}\) thì điện áp hai cuộn cảm L cực đại và \({U_{Lmax}} = \dfrac{{41U}}{{40}}\) . Hệ số công suất tiêu thụ của cả đoạn mạch là:

• A. $0,6$
• B. \(1/\sqrt {15} \)
• C.  \(1/\sqrt {26} \)
• D. $0,8$

Phương pháp giải

Vẽ giản đồ véctơ

Lời giải của GV Loigiaihay.com

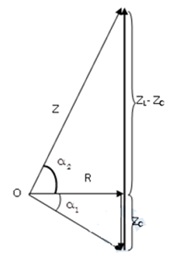
Có thể giả sử: \(Z = 40\Omega ;{Z_L} = 41\Omega \)

Khi đó: \({Z_C} = \sqrt {{{41}^2} - {{40}^2}}  = 9\Omega \)

\(R = \sqrt {2{Z_C}{Z_L} - 2 {Z_C}{Z_C}} \)

Hệ số công suất của mạch khi đó: \({\rm{cos}}\varphi {\rm{ = }}\dfrac{R}{Z} = \dfrac{{24}}{{40}} = 0,6\)

Đáp án : A