Đề bài

Đặt điện \(u{\rm{ }} = {\rm{ }}U\sqrt 2 cos\left( {2\pi ft} \right)\)(U không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Khi tần số là f₁ thì cảm kháng và dung kháng của đoạn mạch có giá trị lần lượt là \(6\Omega \) và \(8\Omega \) . Khi tần số là f₂ thì hệ số công suất của đoạn mạch bằng $1$. Hệ thức liên hệ giữa f₁ và f₂ là:

• A. \({f_2} = \dfrac{4}{3}{f_1}\)
• B. \({f_2} = \dfrac{{\sqrt 3 }}{2}{\rm{ }}{f_1}\)
• C. \({f_2} = \dfrac{2}{{\sqrt 3 }}{f_1}\)
• D. \({f_2} = \dfrac{3}{4}{f_1}\)

Phương pháp giải

Hệ số công suất của đoạn mạch bằng 1 tương đương với \({Z_L} = {Z_C}\)

Lời giải của GV Loigiaihay.com

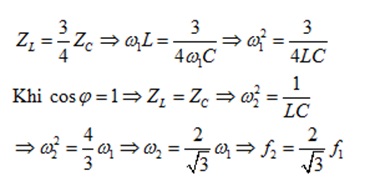
Đáp án : C